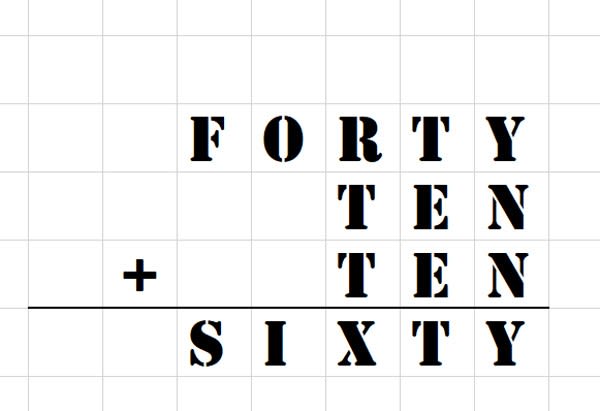
覆面算です。
アルファベットをアラビア数字に変換すると 40+10+10=60 計算成り立ってます。
同じアルファベットには同じ数字が入ります。
数字はそれぞれ0から9のいずれかが1つです。
************************************************************************
先日の解答です。

一桁の異なる数の和は 8+9=17 下の位からの繰り上がりがあっても 8+9+1=18 が最大です。
と言うことで Ⅿ=1 です。

Sは8か9です。S+1 あるいは S+1+1(百の位の和が繰り上がった場合)が10か11ですので。
Oは0か1となります。が、M=1 が確定していますのでO=0です。

E≠N E+0 から N=E+1 がわかります。(十の位から繰り上がった)
また百の位は繰り上がりません。
E=9で十の位からの繰り上がりがあれば可能ですが、そうなるとN=0となりますのでこれはあり得ません。
したがって S=9 となります。

十の位 N+R=10+E あるいは10+E-1(D+Eが繰り上がるとき)です。
NにE+1を代入すると
E+1+R=10+E ・・・ R=9
E+1+R=-10+E-1 ・・・R=8 すでに9は確定しているので R=8 です。
DEは繰り上がることが決定。

残る数は 2・3・4・5・6・7 です。
一のくらいの和 D+E が繰り上がることが解っていて残りの数からYは2以上です。 12≦D+E
DとEの組み合わせは 5・7 6・7 のいずれかです。
E+1=N ですから E=5 ならば N=6 D=7
E=6 ならば N=7 しかしこれは D=6 あるいは D=7・・・これは・・・?。
E=5 が決まりました。
Y=2 となります。
正解は 9567+1085=10652 です。



















