算額(その1623)
~落書き帳「○△□」~ 392.○△□の新算額(その5)
http://streetwasan.web.fc2.com/math18.2.1.html
キーワード:円4個,外円,円弧
#Julia, #Julia, #SymPy, #算額, #和算, #数学
算額(その1622)は,もともとは(注)以下のようなものである。
外円の中に,甲円 1 個,乙円 1 個,丙円 2 個を容れる。外円の直径が与えられたとき,丙円の直径は甲円の直径により変化する。丙円の直径が最大になるのはどのようなときか。また,そのときの直径ははいかほどか。
注:和算の解法ー美しい幾何の問題を解く楽しみー,米山忠興著,開成出版 2012)

外円の半径と中心座標を R, (0, 0)
甲円の半径と中心座標を r1, (0, R - r1)
乙円の半径と中心座標を r2, (0, r2 - R)
丙円の半径と中心座標を r3, (x3, y3)
外円と乙円の交点座標を (x0, y0)
とおき,以下の連立方程式を解き,r2, r3, x3, y3, x0, y0 を求める。
それぞれの解は R と r1 を含む式で表される。
include("julia-source.txt");
# julia-source.txt ソース https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf
using SymPy
@syms R::positive, r1::positive, r2::positive,
r3::positive, x3::positive, y3::positive,
x0::positive, y0::positive
eq1 = x3^2 + (R - r1 - y3)^2 - (r1 + r3)^2
eq2 = x3^2 + (y3 + R)^2 - (r2 + r3)^2
eq3 = x3^2 + y3^2 - (R - r3)^2
#eq4 = (r1 + r2)^2 - ((r1 + r3)^2 + (r2 + r3)^2)
eq5 = 2r1 + r2 - 2R
eq6 = x0^2 + (y0 + R)^2 - r2^2
eq7 = x0^2 + y0^2 - R^2
res = solve([eq1, eq2, eq3, eq5, eq6, eq7], (r2, r3, x3, y3, x0, y0))[1]; # 1 of 2
丙円の半径 r3 は,以下の式のようになり,R は固定された定数で,甲円の半径 r1 により変化する。
# r3
res[2] |> println
r1*(-2*R + r1)*(-R + r1)/(2*R^2 - 2*R*r1 + r1^2)
R = 1/2 のとき,r1 と r3 の関係は以下の図のようになる。r1 が 0.2 ~ 0.3 の間で r3 は最大になる。
pyplot(size=(300, 200), grid=false, aspectratio=:none, label="", fontfamily="IPAMincho")
plot(res[2](R => 1/2), xlims=(0, 1/2), xlabel="r1", ylabel="r3")
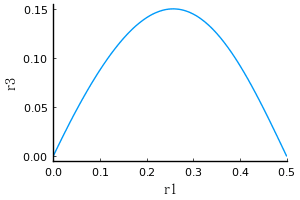
r3 が最大になるときの r1 は,r3 の導関数を求め,方程式「導関数 = 0」をとき,r3 が最大になるときの r1 を求める。
ans_r1 = solve(diff(res[2], r1), r1)[1] # 1 of 4
ans_r1 |> println
R*(1 - sqrt(-2 + sqrt(5)))
R = 1/2 のとき,r1 = 0.257065864121677 のときに r3 は最大になる。
ans_r1(R => 1/2).evalf() |> println
0.257065864121677
r1 = 0.257065864121677 のときの r3 の値は 0.150141553000389 である。
res[2](r1 => 0.257065864121677)(R => 1/2) |> println
0.150141553000389
外円の直径が 1 のとき,甲円の直径が 0.514132 のときに丙円が最大になり,その直径は 0.300283 である。
# r2
res[1] |> println
-2*(-R + r1)
# r3
res[2] |> println
r1*(-2*R + r1)*(-R + r1)/(2*R^2 - 2*R*r1 + r1^2)
# x3
res[3] |> println
-2*sqrt(2)*sqrt(R)*r1*(-R + r1)*sqrt(2*R - r1)/(2*R^2 - 2*R*r1 + r1^2)
# y3
res[4] |> println
(2*R^3 - 4*R^2*r1 + r1^3)/(2*R^2 - 2*R*r1 + r1^2)
# x0
res[5] |> println
-2*sqrt(r1)*(-R + r1)*sqrt(2*R - r1)/R
# y0
res[6] |> println
(R^2 - 4*R*r1 + 2*r1^2)/R
function draw(R, more=false)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
r1 = R*(1 - sqrt(√5 - 2))
r3 = r1*(2R - r1)*(R - r1)/(2R^2 - 2R*r1 + r1^2)
r2 = 2(R - r1)
x3 = 2√2r1*sqrt(R*(2R - r1))*(R - r1)/(2R^2 - 2R*r1 + r1^2)
y3 = (2R^3 - 4*R^2*r1 + r1^3)/(2R^2 - 2R*r1 + r1^2)
x0 = 2sqrt(r1)*(R - r1)*sqrt(2R - r1)/R
y0 = (R^2 - 4R*r1 + 2r1^2)/R
@printf("外円の直径が %g のとき,甲円の直径が %g のときに丙円が最大になり,その直径は %g である。\n", 2R, 2r1, 2r3)
@printf("R = %g; r1 = %g; r2 = %g; r3 = %g; x3 = %g; y3 = %g\n", R, r1, r2, r3, x3, y3)
θ = atand(y0 + R, x0)
println(θ)
plot()
circle(0, 0, R, :green)
circle(0, R - r1, r1)
circle(0, -R, r2, :blue, beginangle=θ, endangle=180 - θ)
circle2(x3, y3, r3, :orange)
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
hline!([0], color=:gray80, lw=0.5)
vline!([0], color=:gray80, lw=0.5)
point(0, R, "R", :green, :center, :bottom, delta=delta/2)
point(0, R - r1, "甲円:r1,(0,R-r1)", :red, :center, delta=-delta)
point(0, -R, "乙円:r2,(0,-R)", :blue, :center, :bottom, delta=2delta)
point(x3, y3, "丙円:r3\n(x3,y3)", :orange, :center, delta=-delta)
end
end;
draw(1/2, true)


















