算額(その113)
(16) 京都府京都市右京区山ノ内宮脇町 山王神社 明治23年(1890)
近畿数学史学会:近畿の算額「数学の絵馬を訪ねて」,平成4年5月16日 初版第一刷,大阪教育図書株式会社,大阪市.
愛媛県松山市吉藤町 三島神社 明治13年(1880)7月
http://www.wasan.jp/ehime/misima.html
兵庫県上郡町 上郡天満神社 文化5年(1808)
https://kamigori-town-museum.jp/cultural-asetts/559/
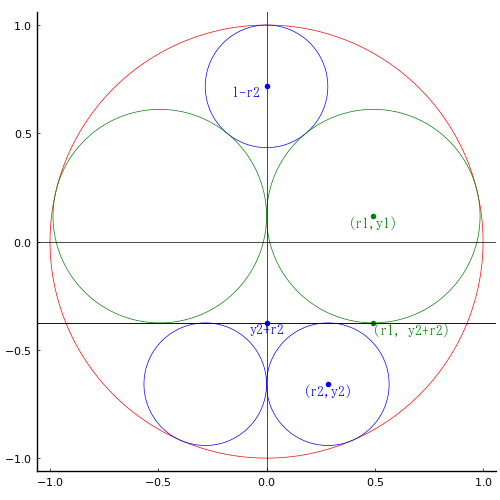
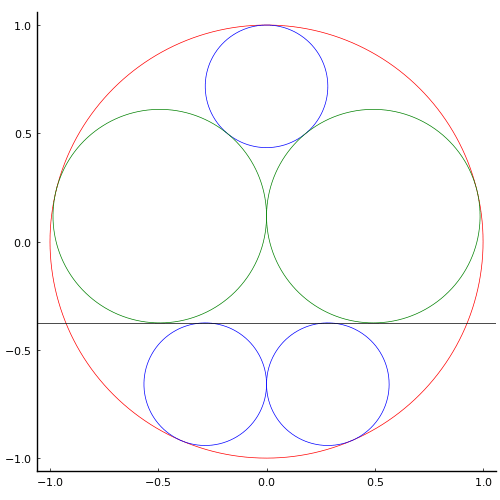
鉤が 108間6合,股が144間8合の直角三角形の内部に円と正三角形が入っている。正三角形の一辺の長さはいかほどか?

鉤股を 1086, 1448 とする。
円の半径を r,正三角形の頂点座標を,x1, (x2, y2), x3 として以下のように記号を定め方程式を解く。

using SymPy
function distance(x1, y1, x2, y2, x0, y0)
p1, p2 = sympy.Point(x1, y1), sympy.Point(x2, y2)
l = sympy.Line(p1, p2)
l.distance(sympy.Point(x0, y0))^2 # 二乗距離を返す!!
end;
@syms r, x1, x2, y2;
eq1 = distance(0, 1086, 1448, 0, r, r) - r^2;
eq2 = (x2 - x1)^2 + y2^2 - 4(x2 - x1)^2 |> expand
eq3 = distance(x1, 0, x2, y2, r, r) - r^2
eq4 = 1448y2 - 1086*(1448 - x2)
res = solve([eq1, eq2, eq3, eq4], (r, x1, x2, y2));
res
8-element Vector{NTuple{4, Sym}}:
(362, 362 - 362*sqrt(3), 5792/13 - 1448*sqrt(3)/13, 1086*sqrt(3)/13 + 9774/13)
(362, 362 - 362*sqrt(3)/3, -1448*sqrt(3)/3, 362*sqrt(3) + 1086)
(362, 362 + 362*sqrt(3), 1448*sqrt(3)/13 + 5792/13, 9774/13 - 1086*sqrt(3)/13)
(362, 362*sqrt(3)/3 + 362, 1448*sqrt(3)/3, 1086 - 362*sqrt(3))
(2172, 2172 - 2172*sqrt(3), 4344 - 2896*sqrt(3), -2172 + 2172*sqrt(3))
(2172, 2172 - 724*sqrt(3), 21720/13 - 8688*sqrt(3)/13, -2172/13 + 6516*sqrt(3)/13)
(2172, 2172 + 2172*sqrt(3), 4344 + 2896*sqrt(3), -2172*sqrt(3) - 2172)
(2172, 724*sqrt(3) + 2172, 8688*sqrt(3)/13 + 21720/13, -6516*sqrt(3)/13 - 2172/13)
for i = 1:8
println("r = $(res[i][1].evalf())")
println("x1 = $(res[i][2].evalf())")
println("x2 = $(res[i][3].evalf())")
println("y2 = $(res[i][4].evalf())")
println()
end
r = 362.000000000000
x1 = -265.002392339934
x2 = 252.614648510790
y2 = 896.539013616908
r = 362.000000000000
x1 = 152.999202553355
x2 = -836.003189786578
y2 = 1713.00239233993
r = 362.000000000000
x1 = 989.002392339934
x2 = 638.462274566133
y2 = 607.153294075400
r = 362.000000000000
x1 = 571.000797446645
x2 = 836.003189786578
y2 = 458.997607660066
r = 2172.00000000000
x1 = -1590.01435403960
x2 = -672.019138719469
y2 = 1590.01435403960
r = 2172.00000000000
x1 = 917.995215320133
x2 = 513.226352603200
y2 = 701.080235547600
r = 2172.00000000000
x1 = 5934.01435403960
x2 = 9360.01913871947
y2 = -5934.01435403960
r = 2172.00000000000
x1 = 3426.00478467987
x2 = 2828.31210893526
y2 = -1035.23408170145
4 番目の解が妥当である。
正三角形の一辺の長さは x1 + 2(x2-x1) = 530.004784679867,もとの単位では 53間強である。
144間8合 × (√3 - 1)/2 = 53.00047846798671 間

using Plots
using Printf
function circle(ox, oy, r, color=:red; beginangle=0, endangle=360)
θ = beginangle:0.1:endangle
x = r.*cosd.(θ)
y = r.*sind.(θ)
plot!(ox .+ x, oy .+ y, color=color, linewidth=0.5)
end;
function point(x, y, string="", color=:green, position=:left, vertical=:top; mark=true)
mark && scatter!([x], [y], color=color, markerstrokewidth=0)
annotate!(x, y, text(string, 10, position, color, vertical))
end;
function segment(x1, y1, x2, y2, color=:black; linestyle=:solid, linewidth=0.5)
plot!([x1, x2], [y1, y2], color=color, linestyle=linestyle, linewidth=linewidth)
end;
function draw(more)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
(r, x1, x2, y2) = res[4]
x3 = x1 + 2(x2 - x1)
plot([0, 1448, 0, 0], [0, 0, 1086, 0], color=:black, lw=0.5)
circle(r, r, r)
segment(x1, 0, x2, y2, :green)
segment(x2, y2, x3, 0, :green)
if more == true
println("x = $(sqrt((x2-x1)^2 + y2^2)) = $((sqrt((x2-x1)^2 + y2^2)).evalf())")
println("x3 - x1 = $(x3 - x1) = $((x3 - x1).evalf())")
point(r, r, "(r,r)", :green, :center)
point(x1, 0, " x1", :green, :left, :bottom)
point(x3, 0, " x3", :green, :left, :bottom)
point(x2, y2, " (x2,y2)", :green, :left, :bottom)
hline!([0], color=:black, lw=0.5)
vline!([0], color=:black, lw=0.5)
end
end;
x = sqrt((-362 + 362*sqrt(3))^2 + (1086 - 362*sqrt(3))^2) = 530.004784679867
x3 - x1 = -724 + 724*sqrt(3) = 530.004784679867