算額（その328）

算額（その328）

埼玉県吉見町 安楽寺 文政5年(1822)
http://www.wasan.jp/saitama/anrakuji.html

菱形の中に直径の同じ 4 個の円を入れる。菱長（長い方の対角線）の二乗と菱横（短い方の対角線）の二乗の和が 400歩，外積（菱形の面積から 4 個の円の面積の和を除いた面積; 図で灰色の部分の面積）が 45.44 歩である。
菱長，菱横，円の直径，菱面（菱形の一辺の長さ）を求めよ。

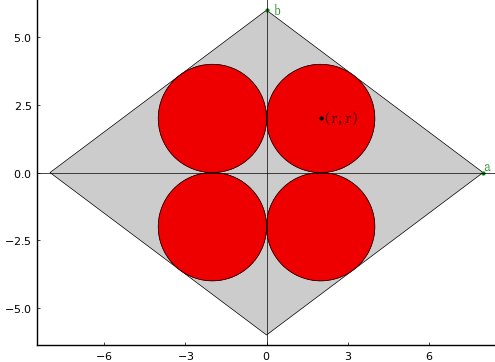
菱長，菱横，円の直径，菱面 を 2a, 2b, 2r とおく。

方程式を解く前に，ここで用いられている円積率（π/4 の近似値，つまり円の面積 ≒ 円積率 * 直径の二乗）は当時広く採用されていた 0.75（すなわち π ≒ 3 とする）ではないので，採用した円積率がいくつなのか調べていく途中で，「吉田光由『塵劫記』(1627)が3.16を使っている」という記述を見つけた（https://www.ndl.go.jp/math/s1/c4.html）。つまり，3.16/4 = 0.79 である。
これによれば「外積が 45.44 歩」という数値の意味がわかる。

a > b なので 2 組目のものが適解である。
すなわち，菱長 = 16寸，菱横 = 12寸, 円径の直径 = 4寸，菱面 = 10寸 である。

include("julia-source.txt");

using SymPy

@syms a::positive, b::positive, r::positive, 菱面::positive;

円積率 = 0.79  # = 3.16/4
eq1 = (2a)^2 + (2b)^2 - 400
eq2 = a + b - sqrt(a^2 + b^2) - 2r
eq3 = 2a*b - 4(円積率*(2r)^2) - 45.44
eq4 = a^2 + b^2 - 菱面^2

res = solve([eq1, eq2, eq3, eq4], (a, b, r, 菱面))

   2-element Vector{NTuple{4, Sym}}:
    (6.00000000000000, 8.00000000000000, 2.00000000000000, 10.0000000000000)
    (8.00000000000000, 6.00000000000000, 2.00000000000000, 10.0000000000000)

using Plots

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (a, b, r, 菱面) = (8, 6, 2, 10)
   plot([a, 0, -a, 0, a], [0, b, 0, -b, 0], linecolor=:black, linewidth=0.5, seriestype=:shape, fillcolor=:gray80)
   circlef(r, r, r, :red2)
   circlef(-r, r, r, :red2)
   circlef(r, -r, r, :red2)
   circlef(-r, -r, r, :red2)
   circle4(r, r, r, :black)
   if more
       point(a, 0, "a", :green, :left, :bottom)
       point(0, b, "   b", :green, :left, :center)
       point(r, r, "      (r,r)", :black, :left, :center)
       vline!([0], color=:black, lw=0.5)
       hline!([0], color=:black, lw=0.5)
   else
       plot!(showaxis=false)
   end
end;

算額（その327）

算額（その327）

埼玉県吉見町 安楽寺 文政5年(1822)
http://www.wasan.jp/saitama/anrakuji.html

鉤股弦に中鉤を引き，二分割された領域に大円と小円が鉤，股，弦，中鉤に内接している。小円の直径は大円の直径より 4 寸短く，弦は股より10 寸長い。
鉤，股，弦，大円の直径，小円の直径を求めよ。

一度に（描画に必要な変数も含めて）全ての変数を求めるのは solve() にとっては重荷なので，要求されている変数だけを求める連立方程式を解く。

include("julia-source.txt");

using SymPy

@syms r1::positive, r2::positive, 鉤::positive, 股::positive, 弦::positive, 長弦::positive, 中鉤::positive;

eq1 = 2r1 -2r2 - 4
eq2 = 中鉤 * 弦 / 2 - 鉤 * 股 / 2
eq3 = 長弦 + 中鉤 - 股 - 2r1
eq4 = (弦 - 長弦) + 中鉤 - 鉤 - 2r2
eq5 = 鉤^2 + 股^2 - 弦^2
eq6 = 弦 - 股 - 10
eq7 = 中鉤/長弦 - 鉤/股

res = solve([eq1, eq2, eq3, eq4, eq5, eq6, eq7], (鉤, 股, 弦, r1, r2, 中鉤, 長弦))

   1-element Vector{NTuple{7, Sym}}:
    (30, 40, 50, 8, 6, 24, 32)

鉤 = 30寸，股 = 40寸，弦 = 50寸，大円直径 = 16寸，小円直径 = 12寸である。

図を描くために，大円と小円の中心座標 (x1, r1), (股 - r2, y2) の 2変数 x1, y2 を求める連立方程式を解く（鉤，股，r1, r2 は前段階の結果を引き継ぐ）。
結果は 2 通り得られるが，最初のものが適解である。

@syms r1::positive, r2::positive, 鉤::positive, 股::positive, 弦::positive, 長弦::positive, 中鉤::positive,
   x1::positive, y2::positive;

(鉤, 股, 弦, r1, r2, 中鉤, 長弦) = (30, 40, 50, 8, 6, 24, 32)
eq8 = distance(0, 0, 股, 鉤, x1, r1) - r1^2
eq9 = distance(0, 0, 股, 鉤, 股 - r2, y2) - r2^2
res2 = solve([eq8, eq9], (x1, y2))

   2-element Vector{Tuple{Sym, Sym}}:
    (24, 18)
    (24, 33)

using Plots

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (鉤, 股, 弦, r1, r2, 中鉤, 長弦) = (30, 40, 50, 8, 6, 24, 32)
   (x1, y2) = (24, 18)
   (x, y) = 長弦 .* (4/5, 3/5)  # 弦と中鉤の交点座標（弦と中鉤は直交する）
   plot([0, 股, 股, 0], [0, 0, 鉤, 0], color=:black, lw=0.5)
   circle(x1, r1, r1)
   circle(股 - r2, y2, r2, :blue)
   segment(x, y, 股, 0, :green)
   if more
       point(x1, r1, "\n大円:r1\n(x1, r1)", :red, :center)
       point(股 - r2, y2, "\n小円:r2\n(股-r2,y2)", :blue, :center)
       point(股, 0, " A", :black, :left, :bottom)
       point(股, 鉤, " B", :black)
       point(0, 0, "   O", :black, :left, :bottom)
       point(x, y, "C ", :black, :right, :bottom)
       annotate!(10, 20, text("AB: 鉤\nAO: 股\nBO: 弦\nAC: 中鉤\nCO: 長弦", :left, 10))
       vline!([0], color=:black, lw=0.5)
       hline!([0], color=:black, lw=0.5)
   else
       plot!(showaxis=false)
   end
end;