算額(その346)
岐阜県大垣市赤坂町 金生山明星輪寺 元治2年(1865)http://ryugen3.sakura.ne.jp/toukou3/wasankibousya.PDF
扇の中に赤円,緑円,白円を入れる。扇の半径を与えて,白円が最大となるとき,赤円と白円との直径の和を求めよ。
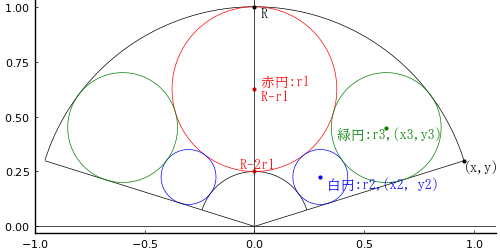
扇の要を原点とし,扇の半径を R
赤円の直径を r1, (0, R - r1)
白円の直径を r2, (x2, y2)あ
緑円の直径を r3, (x3, y3)
とする。
include("julia-source.txt");
using SymPy
R = 1 とおき,赤円,白円,緑円の半径を決める。
緑円の半径は R - 2r1 + 2r2 + 2r3 = R なので,r3 = r1 - r2 である。
@syms R::positive, x::positive, r1::positive, r2::positive, x2::positive, y2::positive,
r3::positive, x3::positive, y3::positive
solve(R - 2r1 + 2r2 + 2r3 - R, r3);
r3 = r1 - r2
白円と緑円の中心は原点を通る直線上にある。この直線と扇の右端の直線のなす角を θ とする。
原点から白円と緑円中心までの距離はそれぞれ 1 - 2r1 + r2, 1 - 2r1 + 2r2 + r3 である。
よって
r2 = (1 - 2r1 + r2)sin(θ)
r3 = (1 - 2r1 + 2r2 + r3)sin(θ) である(つまり,r2, r3 を一辺とする直角三角形は相似である)。
これより,r2/r3 = (1 - 2r1 + r2)/(1 - r3) である。
eq0 = r2/r3 - (1 - 2r1 + r2)/(1 - r3) |> expand
eq0 |> println
2*r1/(-r1 + r2 + 1) - r2/(-r1 + r2 + 1) + r2/(r1 - r2) - 1/(-r1 + r2 + 1)
この式を r2 について解くと,2つの解が得られるが 2 番目のもの r1 + sqrt(1 -2r1)/2 -1/2 が適解である。
solve(eq0, r2)
r2 = r1 + sqrt(1 -2r1)/2 - 1//2
これを r1 の関数とみて,極大値・最大値を求めるには,まず r1 について微分し,微分係数 = 0 となる r1 を求める。
plot(r2, xlims=(0, 0.5), ylims=(0, 0.15), xlabel="r1", ylabel="r2", aspectratio=:none)
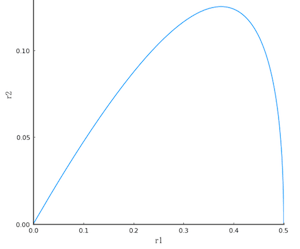
diff(r2)
d = 1 - 1/2sqrt(1 - 2r1)
plot(d, xlims=(0, 0.5), ylims=(-0.1, 0.5), xlabel="r1", ylabel="r2'", aspectratio=:none)
hline!([0])
plot!()
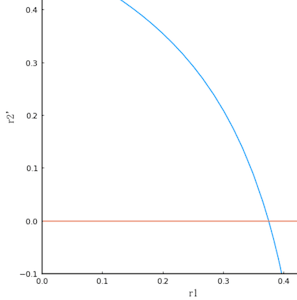
d = 1 - 1/2sqrt(1 - 2r1) = 0 を解いて,r1 = 3/8 のときに r2 が最大値 1/8 をとる。
r1 = 3/8 のとき極大かつ最大値をとる。
solve(eq0(r1 => 3//8))[1] |> println # r2
1/8
赤円の直径と白円の直径の和は 2\*3/8 + 2\*1/8 = 1。つまり,白円が最大となるとき,赤円と白円の直径の和は扇の半径に等しい。
また,r3 = r1 - r2 なので,r3 = 2/8 である。
次に,各円の中心座標と扇の右端の点の座標を求める。
using SymPy
@syms R::positive, x::positive, x2::positive, y2::positive,
r3::positive, x3::positive, y3::positive
R = 1
(r1, r2) = (3//8, 1//8)
r3 = r1 - r2
eq1 = x2^2 + (R - r1 - y2)^2 - (r1 + r2)^2
eq2 = x3^2 + (R - r1 - y3)^2 - (r1 + r3)^2
eq4 = x2^2 + y2^2 - (r2 + R - 2r1)^2
eq5 = x3^2 + y3^2 - (R - r3)^2
eq6 = distance(0, 0, x, sqrt(R^2 - x^2), x2, y2) - r2^2;
eq7 = distance(0, 0, x, sqrt(R^2 - x^2), x3, y3) - r3^2;
solve([eq1, eq2, eq4, eq5, eq6], (x, x2, y2, x3, y3))
2-element Vector{NTuple{5, Sym}}:
(-1/5 + 8*sqrt(2)/15, 3/10, 9/40, 3/5, 9/20)
(1/5 + 8*sqrt(2)/15, 3/10, 9/40, 3/5, 9/20)
2 番目のものが適解である。
扇の中心角 = 145.203°
赤円半径 = 0.375; 白円半径 = 0.125; 緑円半径 = 0.25
x = 0.954247; x2 = 0.3; x3 = 0.225; x3 = 0.6; y4 = 0.45
赤円直径 + 白円直径 = 1 すなわち,赤円の直径と白円の直径の和は扇の半径に等しい
以上の結果に基づき図を描く。
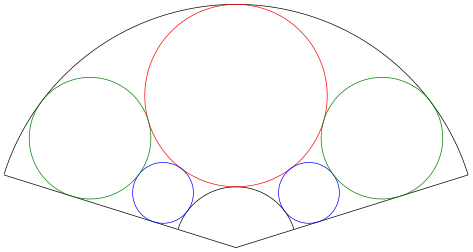
function draw(more)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
R = 1
(r1, r2) = (3//8, 1//8)
r3 = r1 - r2
(x, x2, y2, x3, y3) = (1/5 + 8*sqrt(2)/15, 3/10, 9/40, 3/5, 9/20)
y = sqrt(R^2 - x^2)
r3 = r1 - r2
θ = atand(y, x)
@printf("扇の中心角 = %g°\n", 180 - 2θ)
@printf("赤円半径 = %g; 白円半径 = %g; 緑円半径 = %g\n", r1, r2, r3)
@printf("x = %g; x2 = %g; x3 = %g; x3 = %g; y4 = %g\n", x, x2, y2, x3, y3)
@printf("赤円直径 + 白円直径 = %g\n", 2r1 + 2r2)
plot()
circle(0, 0, R, :black, beginangle=θ, endangle=180 - θ)
circle(0, 0, R - 2r1, :black, beginangle=θ, endangle=180 - θ)
segment(0, 0, x, y, :black)
segment(0, 0, -x, y, :black)
circle(0, R - r1, r1, :red)
circle(x2, y2, r2, :blue)
circle(-x2, y2, r2, :blue)
circle(x3, y3, r3, :green)
circle(-x3, y3, r3, :green)
if more
point(0, R, " R", :black)
point(x, y, "(x,y)", :black)
point(0, R - r1, " 赤円:r1\n R-r1", :red, :left, :vcenter)
point(0, R - 2r1, " R-2r1", :red, :center, :bottom)
point(x3, y3, " 緑円:r3,(x3,y3)", :green, :center)
point(x2, y2, " 白円:r2,(x2, y2)", :blue)
hline!([0], color=:black, lw=0.5)
vline!([0], color=:black, lw=0.5)
else
plot!(showaxis=false)
end
end;



















