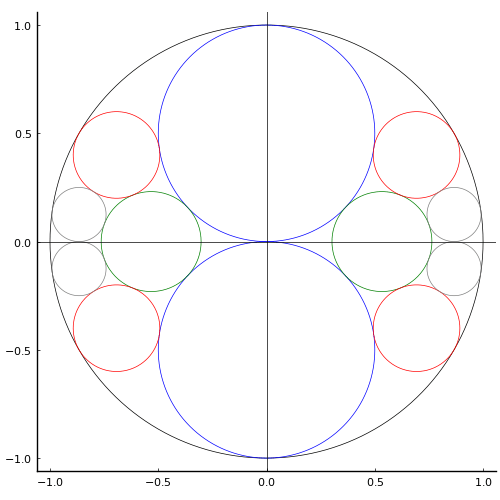
算額(その351)
岐阜県大垣市赤坂町 金生山明星輪寺 元治2年(1865)
http://ryugen3.sakura.ne.jp/toukou3/wasankibousya.PDF
正三角形と外円との間に,緑円,赤円,白円を計 16 個をいれる。正三角形の内接円の半径が与えられたとき白円の直径を求めよ。
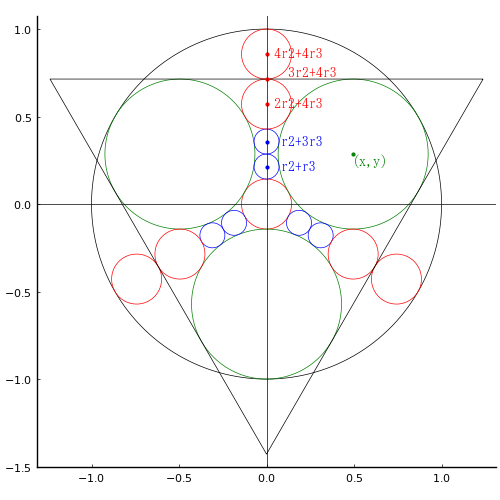
記述を簡潔にできるように元の図を上下反転させて考える。
緑円の半径と中心座標 r1, (x, y)
赤円の半径と中心座標 r2, (0, 0), (0, 2r2 + 4r3), (0, 4r2 + 4r3)
白円の半径と中心座標 r3, (0, r2 + r3), (0, r2 + 3r3)
外円の半径と中心座標 r0, (0, 0); r0 = 5r2 + 4r3
正三角形に内接する円の半径は 3r2 + 4r3
外円の半径を 1 として他の変数の値を求め,r2, r3 を求め,r2 と 3r2 + 4r3 の比を求める。
include("julia-source.txt");
using SymPy
@syms r0::positive, r1::positive, r2::positive, r3::positive, x::positive, y::positive;
r0 = 1
y = r2 + 2r3
r1 = 2r2 + 2r3
eq1 = x^2 + y^2 - (r1 + r2)^2
eq2 = x^2 + (y - r2 - r3)^2 - (r1 + r3)^2
eq3 = 5r2 + 4r3 - r0
res = solve([eq1, eq2, eq3], (r2, r3, x))
1-element Vector{Tuple{Sym, Sym, Sym}}:
(1/7, 1/14, 2*sqrt(3)/7)
r0 = 1; r1 = 0.428571; r2 = 0.142857; r3 = 0.0714286; x = 0.494872, y = 0.285714
正三角形に内接する円の半径 = 0.714286
白円の半径 = 0.0714286
赤円,白円の半径はそれぞれ 1/7, 1/14。
正三角形の内接円の半径は 3r2 + 4r3 = 3/7 + 4/14 = 10/14。
よって,白円の半径は正三角形の内接円の半径の 1/10 である。
using Plots
function draw(more)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
(r2, r3, x) = res[1]
r0 = 1
y = r2 + 2r3
r1 = 2r2 + 2r3
@printf("r0 = %g; r1 = %g; r2 = %g; r3 = %g; x = %g, y = %g\n", r0, r1, r2, r3, x, y)
@printf("正三角形に内接する円の半径 = %g\n", 3r2 + 4r3)
@printf("白円の半径 = %g\n", r3)
plot()
circle(0, 0, r0, :black)
circle(0, 0, r2)
rotate(x, y, r1, :green)
rotate(0, r2 + r3, r3, :blue)
rotate(0, r2 + 3r3, r3, :blue)
rotate(0, 2r2 + 4r3, r2)
rotate(0, 4r2 + 4r3, r2)
ic = 3r2 + 4r3
plot!([√3ic, -√3ic, 0, √3ic], [ic, ic, -2ic, ic], color=:black, lw=0.5)
if more
point(x, y, "(x,y)")
point(0, r2 + r3, " r2+r3", :blue, :left, :vcenter)
point(0, r2 + 3r3, " r2+3r3", :blue, :left, :vcenter)
point(0, 2r2 + 4r3, " 2r2+4r3", :red, :left, :vcenter)
point(0, 3r2 + 4r3, " 3r2+4r3", :red, :left, :bottom)
point(0, 4r2 + 4r3, " 4r2+4r3", :red, :left, :vcenter)
hline!([0], color=:black, lw=0.5)
vline!([0], color=:black, lw=0.5)
else
plot!(showaxis=false)
end
end;