算額(その1605)
新潟県長岡市 悠久山 享和元年(1801)
深川英俊,トニー・ロスマン:聖なる数学:算額,森北出版株式会社,2010年4月22日.
キーワード:円5個,外円,弦,矢,斜線2本
#Julia, #SymPy, #算額, #和算, #数学
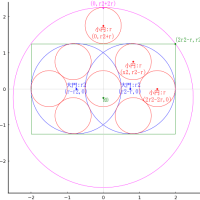
外円の中に,弦,矢,斜線,甲円,乙円を容れる。外円の直径が与えられ,「弦 - 矢」が最大になるとき,乙円の直径はいかほどか。

弦,矢をそのまま変数名とする。
外円の半径と中心座標を R, (0, 0)
甲円の半径と中心座標を r1, (0, R - 矢 + r1), (0, R - r1)
乙円の半径と中心座標を r2, (x2, R - 矢/2)
斜線と外円の交点座標を (x0, y0)
とおき,以下の連立方程式を解く。
まず初めに,「『弦 - 矢』が最大になるとき」という条件を解決する。
弦 = 2sqrt(R^2 - (R - 矢)^2) なので,
差 = 2sqrt(R^2 - (R - 矢)^2) - 矢 である。
矢について導関数を取り,導関数 = 0 をとき,矢を求める。
include("julia-source.txt");
# julia-source.txt ソース https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf
using SymPy
@syms 矢::positive, 弦::positive, R::positive,
r1::positive, r2::positive, x2::positive
差 = 2sqrt(R^2 - (R - 矢)^2) - 矢;
ans_矢 = solve(diff(差, 矢), 矢)[1]
ans_矢 |> println
R*(5 - sqrt(5))/5
矢 = R*(5 - √5)/5 である。弦 = 2sqrt(R^2 - (R - 矢)^2) を条件に加え,以下の連立方程式を解く。
@syms 矢::positive, 弦::positive, R::positive,
r1::positive, r2::positive, x2::positive,
x0::positive, y0::positive
矢 = R*(5 - √Sym(5))/5
弦 = 2sqrt(R^2 - (R - 矢)^2) |> simplify
eq1 = dist2(弦/2, R - 矢, 0, R - 矢/2, 0, R - r1, r1)
eq2 = x2^2 + (R - 矢/2)^2 - (R - r2)^2 |> expand |> simplify;
eq3 = r2/x2 - 矢/2/sqrt((弦/2)^2 + (矢/2)^2);
eq4 = (y0 - (R - 矢))/(弦/2 + x0) - 矢/弦
eq5 = x0^2 + y0^2 - R^2
res = solve([eq1, eq2, eq3, eq4, eq5], (r1, r2, x2, x0, y0))[1];
# r2: 乙円の半径
res[2] |> println
-R*(-sqrt(2) + sqrt(10))*(-2*sqrt(2590 - 710*sqrt(5)) + sqrt(11 - sqrt(5))*(-5*sqrt(2) + 5*sqrt(10)))/(160*sqrt(11 - sqrt(5)))
R の倍数であるが,式中に R があるので式が簡約化できない。
倍数だけを取り出して簡約化すると,非常に簡潔な式 R*(5 - √5)/20 になる。
@syms d
apart(res[2]/R, d) |> simplify |> factor |> println
-(-5 + sqrt(5))/20
深川は R/(5 + √5) としているが,分母を有理化すれば同じ式である。
R/(5 + √Sym(5)) |> simplify |> factor |> println
-R*(-5 + sqrt(5))/20
function draw(R, more=false)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
矢 = R*(5 - √5)/5
弦 = 2sqrt(R^2 - (R - 矢)^2)
(r1, r2, x2, x0, y0) = (-2*R - 2*sqrt(5)*R/5 - 2*sqrt(145)*R*sqrt(7 - 2*sqrt(5))/(5*(-7 + 2*sqrt(5))), -R*(-sqrt(2) + sqrt(10))*(-2*sqrt(2590 - 710*sqrt(5)) + sqrt(11 - sqrt(5))*(-5*sqrt(2) + 5*sqrt(10)))/(160*sqrt(11 - sqrt(5))), -R*(-2*sqrt(2590 - 710*sqrt(5)) + sqrt(11 - sqrt(5))*(-5*sqrt(2) + 5*sqrt(10)))/80, -11*sqrt(5)*R/145 - R/29 + sqrt(5)*R*sqrt(870 - 350*sqrt(5))/580 + sqrt(5)*R*sqrt(174 - 70*sqrt(5))/116 + 11*R*sqrt(870 - 350*sqrt(5))/580 + 11*R*sqrt(174 - 70*sqrt(5))/116, sqrt(5)*R*sqrt(870 - 350*sqrt(5))/580 + 11*R*sqrt(870 - 350*sqrt(5))/580 + 16*sqrt(5)*R/145 + 12*R/29)
@printf("R = %g; r1 = %g; r2 = %g; x2 = %g\n", R, r1, r2, x2)
plot()
circle(0, 0, R, :green)
circle2(x2, R - 矢/2, r2)
circle(0, R - r1, r1, :blue)
circle(0, R - 矢 + r1, r1, :blue)
segment(-弦/2, R - 矢, 弦/2, R - 矢, :magenta)
segment(0, R, 0, R - 矢, :magenta)
segment(-弦/2, R - 矢, x0, y0, :magenta)
segment(弦/2, R - 矢, -x0, y0, :magenta)
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
hline!([0], color=:gray80, lw=0.5)
vline!([0], color=:gray80, lw=0.5)
point(0, R, "R", :green, :center, :bottom, delta=delta/2)
point(0, R - 矢/2, "R-矢/2", :magenta, :right, :vcenter, deltax=-4delta)
point(0, R - 矢 + r1, "甲円:r1,(0,R-矢+r1)", :blue, :center, delta=-delta)
point(0, R - r1, "甲円:r1,(0,R-r1)", :blue, :center, :bottom, delta=delta/2)
point(x2, R - 矢/2, "乙円:r2,(x2,R-矢/2)", :red, :center, delta=-delta/2)
point(弦/2, R - 矢, "(弦/2,R-矢)", :magenta, :right, delta=-delta/2)
end
end;
draw(1/2, true)