有意水準 20% はナシ

「A/Bテストの数理」への批判
http://abrahamcow.hatenablog.com/entry/2013/12/28/210035
だけどねえ。ちょっといただけない。

ではこの場合、有意水準はいくつくらいにしたらいいんでしょうか？

とてもよい質問です。
たぶん20％くらいでいいんじゃないかと思います。

その根拠は天気予報です。
降水確率0％～20％くらいならだいたいみんな傘持ってかないじゃないですか。
40％～100％ならだいたいみんな傘持っていくんじゃないでしょうか。
30％だと人によってはちょっと迷うと思います。

だから20％で切っちゃいましょう。
そのくらいのざっくりした感じで十分だと思います。

有意水準は，リスク・ベネフィットの観点を考慮するというのはあたりまえなんですけど，どんな場合でも天気予報のリスク・ベネフィットが当てはまるという認識はおかしい。有意水準は別の見方からいう「危険率」または「第一種の過誤（αエラー）」。これを称して，「あわてん坊のアルファ」ともいう。20％もの危険率を受容していると，とんでもないことになることも多くなるのだけど？？

また，有意水準 5％ は，「統計学における慣例」なので，特に理由がない場合は 5% を採用するのが無難。「有意水準をちゃんと書いた上で有意差ありかなしかを言え」というのはごもっとも。しかし，「有意水準 x% のもとで ●● 検定を行ったところ有意な差があった」などの陳述は，統計検定を知らない人に余計な抵抗感を与えるであろう。5% 有意水準が慣例であるという前提で，「統計学的に意味のある差だった」と述べるのは，許されると思う。

後ろの方にある，「20％ 有意」というのは，聞いたことがない。日本の心理学分野で「10％ で【有意傾向】」というのさえ批判対象になるのだから。

更にいえば，リスク・ベネフィットの判断は極端にいえば個人レベルで差があるので，画一的な有意水準を設けて有意だの有意でないだの言っても意味がない。そのためにはどうするか。答えは，常に P 値を表記するということである。日本ではいまでも，「5％有意」あるいは，星祭りでもないのに「*」だの「**」を併記して自己満足に浸っている（ちなみに，有意傾向はR でも '.' で表されたりすることもある）。欧米諸国では，ずっと前から P 値を表記するのが標準である。

そもそも，更に更にいえば，白か黒かの二値判断（検定）ではなく，「信頼区間を表示しましょう」というのが世界標準だ。日本はこのレベルまでまだ至っていない。

信頼区間は prop.test(..., conf.level = 0.95)$conf.int で得られる。信頼率は conf.level で与えられ，0.95 がデフォルトになっているのは前述の通り「慣例」だからである。

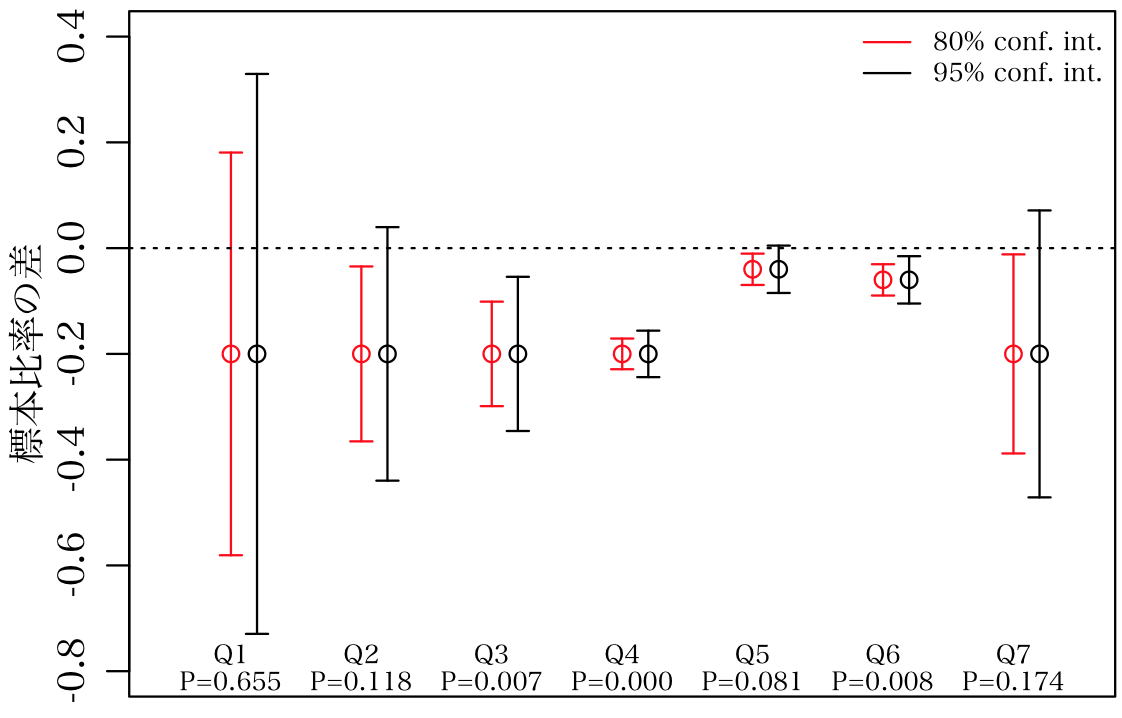
以下の図は，信頼区間を描いたもの。赤は80％信頼区間（有意水準20％と等価），黒は95％信頼区間（有意水準が普通の95％）。信頼区間が0を含まなければ，「有意水準の下で有意差があった」ということと同じ。