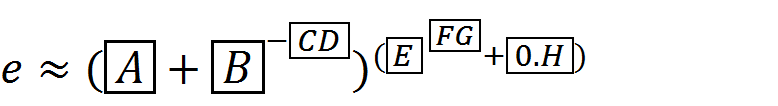三角形の種類はいくつか

円周上を n 等分する点を，順に「点 1」から「点 n」とする。
これらの点から m 個の点を選ぶ（ m ≦ n ）。
m 個の点において，その内の 3 個の点を頂点とする三角形は mC3 個あるが，形の異なるものはいくつあるか。ただし，裏返さずに回転してぴったり重ねられる三角形は同じものとする。
添付図は，n=8，m=5 で，選ばれる点が 1，3，4，6，7 の場合である。

a, j は同じ形
b, d, e は同じ形
f, g は同じ形
残り c, h, i は，他に同じものはない
よって，形の異なる三角形は 6 種類

以下がプログラム。

dist = function(x) {
  p = pos[x]
  d = combn(3, 2, function(y) {
        res = abs(p[y[1]]-p[y[2]])
        ifelse(res > n %/% 2, n-res, res)
        })
  min.pos = which.min(d)
  if (min.pos == 3) d[c(3, 1, 2)]
  else if (min.pos == 2) d[c(2, 3, 1)]
  else if (d[1] == d[3]) d[c(3, 1, 2)]
  else d
}

n = 26 で，全ての点を使ってできる三角形の種類は

> n = 26
> pos = 1:n
> nrow(unique(t(combn(length(pos), 3, dist))))
[1] 100

combn の FUN 引数で定義する関数に注意

かなり，はまった。簡単な例を挙げよう。

combn(10, 5, function(x) print(sum(x)))

は無問題だが，

combn(10, 5, function(x) cat(sum(x)))

は
　　以下にエラー matrix(r, nrow = len.r, ncol = count) :
   'data' はベクトル型でなくてはなりませんが、'NULL' でした

となる。function が値を返さない（cat など）ときは，

combn(10, 5, function(x) cat(sum(x)), simplify=FALSE)

とでもする必要がある。

総当たり足し算

図のような，「サグラダ・ファミリア」の「受難のファサード」にある魔方陣で下記の条件で足し算をした結果，その和が同じになる組み合わせが最も多くなるような値(和)を求めよ。
　　・足し合わせるのは、縦、横、斜めに限らない
　　・足し合わせる数字の個数は4つに限らない



library(e1071)
d = bincombinations(16)
w = c(1, 14, 14, 4, 11, 7, 6, 9, 8, 10, 10, 5, 13, 2, 3, 15)
freq = table(apply(d, 1, function(x) sum(x*w)))
freq[which.max(freq)]

実行結果は，

  66
1364

つまり，和が 66 になる場合が一番多く，1364 通りである。

Hello world! を出力するプログラム

まあ，2 つの言語である文字列を書けということだけど，むしろ同じ言語でどんなバリエーションがあるかのほうが面白いんだろうなあ。

コマンドラインでやる。一行野郎だ。

R でちょっと凝ったやり方？

Rscript -e 'cat(rawToChar(as.raw(c(73, 32, 108, 111, 118, 101, 32, 121, 111, 117, 46))), "\\n")'

I love you.

AWK はあまり，凝ったやり方が思い浮かばなかったので，ずるっこなやり方でごまかす。

gawk 'BEGIN{print "I love you."}'

I love you.

ネイピア数(e)の近似式

A ～ H に 1 から 8 までの数字をあてると、式の結果が自然対数の底、ネイピア数(e=2.7182818284590…)に極めて近い値となる。

まあ，虫食い算ではある。しかし，一筋縄ではいかぬ。

n を大きくすると，e ≒ (1+1/n)^n になるということを利用したもの。
B^(10*C+D) と E^(10*F+G) が（ほぼ同じ大きさで）べらぼうに大きな数になるように，決める。A=1 で，H はゴミ。

library(e1071)
d = permutations(8)
colnames(d) = LETTERS[1:8]
a = d[,2]^(d[,3]*10+d[,4])
b = d[,5]^(d[,6]*10+d[,7])
c = abs(a-b)
unique(d[c == 0, 2:7])

     B C D E F G
[1,] 2 7 6 4 3 8
[2,] 2 3 6 4 1 8
[3,] 4 1 8 2 3 6
[4,] 4 3 8 2 7 6

2^76 == 4^38 = 75557863725914323419136
2^36 == 4^18 = 68719476736

どちらでもよいけど，大きい方がよいだろう。

(1 + 2^(-76)) ^ (4^38 + 0.5) でよいだろう。

> library(Rmpfr)
> (1+mpfr(2^-76, 10000))^(4^38+0.5)
1 'mpfr' number of precision  10000   bits 
[1] 2.71828182845904523536026948327243884562017542260751355373386591261370824199370367512673498355740221866300150192512577013712402194525729088107603625695791765621277477110787864123095526391463127114520685536306474105328349829970690292025415223570462246776367494240117044146359689778284658748377053631108528524369649708990088499705308087739188743458948765814067112847980775789601385668978369082970614962359622188612525084100685222682523211422142283833500680692953117870857304240655781007179275504357626794755609455702336615836088456321464184491100070840364060583518742678339843281161018070243859730035061281270650049058577898918962636823041601318514133991899068659175614049936572365313687224918238106256134904163514252685340647340456890314801271060284733277103452154217953947794212256610001859188824305819005493101420995707315149924255908483971356622254440811665861497806433425245530414577413150274475908707244099490588998007971471915652104821918366705834682993754472524280666636135840177290124580033865188449321263327246243517903169586281573699595084163491236453339564455102365405626778182944392138305434444792827055459439497524425904694000237296631033220159598665136864124246396854272963872820317637333769237193242884202568303364418046273435762454117040706608172930748692315119997997841619429686669820862061110068904028565437826781936159992926487440700174612607470999978707697207082787868267520682657954314633255397701954003355903287968237899866164531903161262850661513441425018870844607137295088827744560605904851144463845968530092277811965079409662380103667771723922279391991904178680345914824907021940796420741369938414632649949272385757279737779566836807257955131811102861602826936065959718009010543032829786047163352214962220611887790481846213267329885769701504016942449439825975274239480548636777535688113115286363107890608944546004286395664234621620727850509634845140884460424113809699482972677973864783637850054751653120718800418467312735020003534712022848421166354423545617401554314100709757290349151738731506203567718721798205167916146075161513837519243811057993341024401841139508335521579606091693535359204092916638388380674274980856483447553569646936493930811895678168317661540052904197578737606560554891406196968343986453614462329059943329291691296011434571917668237269127335807768840376797480758223346640014402206484032202724578013542472530555454711911214217977945257047510183549101102775973480564986345641104547537979739157453386815737096359570223404164680296807328667655874844462658801682855771290628496762097876608805420529910640789738394606194141138693883902905388877002919338757647512180506028142016641093968849053875292720095305141013750955950014732924418826737952161667833410486719424913741594089595708283399701258904526782568491372754701118896742792090433744556255065162659355857680625978388657011433036136201159872406077243795651120889127932226093230037111704708148334727141931962344248175205214809447454142671052905204264772129669310850553225577837867783253200036289105779201198217449032195

フィボナッチ数列（またか）

1,1,2,3から始まるフィボナッチ数列の100桁目の数字は何か

n = 30
fib = integer(n)
fib[1] = fib[2] = 1
for (i in 3:n) {
  fib[i] = fib[i-1]+fib[i-2]
}
ans = paste(fib, collapse="")
if (nchar(ans) >= 100) {
  substring(ans, 100, 100)
}

    

最大公約数で公開鍵を生成

1 から 100 までの素数を 2 つ選び，それぞれ p, q とする。
以下の 2 つの条件を満たす自然数 e が p + q 個になるような p, q の組み合わせをすべて求めよ。

条件１：0 < e < (p - 1)(q - 1)
条件２：gcd((p - 1)(q - 1), e) = 1
　　　( (p - 1)(q - 1) と e の最大公約数が 1 である)

普通に書いても，この程度の計算量なら，簡単に求めることができるのだが。

prime = c(2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97)

euclid = function(m, n) {
  repeat {
    mod = m %% n
    if (mod == 0) return(n)
    m = n
    n = mod
  }
}

func = function(x, y) {
  count = 0
  for (e in seq_len((x-1)*(y-1)-1)) {
    count = count+(euclid((x-1)*(y-1), e) == 1)
  }
  count
}

for (i in 1:(length(prime)-1)) {
  for (j in (i+1): length(prime)) {
    if (func(prime[i], prime[j]) == prime[i]+prime[j]) {
      print(c(prime[i], prime[j]))
    }
   
}

一行野郎（2）

180 以上 189 以下の 10 個の整数の中から異なる 3 個 a, b, c を選び，和が 560 になる組み合わせを全て求めるワンライナーを書け。

Rscript -e "n = 180:189; a = 179+which(outer(outer(n, n, '+'), n, '+') == 560, arr.ind=TRUE); b = a[,1] < a[,2] & a[,2] < a[,3]; a[b,]"
     dim1 dim2 dim3
[1,]  185  187  188
[2,]  185  186  189
[3,]  184  187  189
[4,]  183  188  189

以下の方が，短いか。

Rscript -e "a = expand.grid(180:189, 180:189, 180:189); a[rowSums(a)==560 & a[,1] < a[,2] & a[,2] < a[,3],]"
    Var1 Var2 Var3
876  185  187  188
966  185  186  189
975  184  187  189
984  183  188  189

一行野郎

異なる 3 桁の整数 a, b, cが，以下の条件を満たすとき，a, b, c を求めるワンライナーを書け
   1. aはbより261小さい。
   2. aはcより333大きい。
   3. cはbの100の位の数と一の位の数を入れ替えた数である。
   4. aは7の倍数である。
まあ，結果出力が微妙だけど。
Rscript -e "a = 7*1:(999 %/% 7); c = a - 333; b = a + 261; x = c >= 100 & b <= 999 & c %% 10 == b %/% 100 & b %% 10 == c %/% 100; cbind(a[x], b[x], c[x])"
     [,1] [,2] [,3]
[1,]  490  751  157
[2,]  581  842  248
[3,]  672  933  339

A/B テストには気をつけろ

http://postd.cc/optimizely-got-me-fired/

生兵法は大怪我のもと

言語の得手・不得手

国語・数学・英語・社会・理科5科目の採点結果が、CSVファイルに保存されています。5科目合計点の順位をそれぞれ算出し、結果をCSVファイルとして出力する。 プログラミング言語は、PHPを使ってください。 点数が高い順に、1, 2, ...と順位をつけるだけですが、同じ得点が2人以上の場合は同じ順位になり、それより下の点数は順位がずれていきます。 たとえば、80点が5位で2人いたとすると、79点の人は6位ではなく7位になります。80点が3人いれば、8位になります。 国語・数学・英語・社会・理科の順位に加えて、合計点の順位も出力する。

世間でよくある順位付け。ちっとも，特殊ではない。どうせなら，5e1000000000 人の順位付けをやらせればよいのに。

fileEncoding="cp932" は，Windows の呪い。

 

d = read.csv("class_3c_input.csv", fileEncoding="cp932", row.names=1)
d$合計 = rowSums(d)
d2 = sapply(-d, rank, ties.method="min")

簡単に問題を解ける言語を選ぶのも能力のうちということか。

真意は何処に

 > フィボナッチ数列で500を超えるまでに何個の数値を記述する必要があるか

どうせなら，「5e100 を超えるまでに」とかいえばよいのに（^_^）

せめて，「最小文字数で」とか

a = b = 1
n = nchar(a) + nchar(b)
repeat {
  c = a + b
  cat(c)
  n = n + nchar(c)
  if (c > 500) {
    cat(n)
    break
  }
  a = b
  b = c
}

ユークリッドの互除法の計算過程

1 から整数 n までの間の数から二数を選びユークリッドの互除法で最大公約数を求めるとき，割り算の回数が最大になる二数の組み合わせを求めよ

いくつかの n について，答の二数を求め，その二数にユークリッドの互除法を適用したときの二数の変化の様子を書き出してみる。例えば n = 100 のときは (89, 55) というのが一つの解。

回数        x         y
9          89        55
8          55        34
7          34        21
6          21        13
5          13         8
4           8         5
3           5         3
2           3         2
1           2         1

これが除算回数が一番多いのならば，次に除算回数が大きい二数は？(89+55, 89) = (144, 89)

つまり，二数は，
a[1] = 1
a[2] = 2
a[n]=a[n-1]+a[n-2],  n ≧ 3 という数列の相隣り合う二数ということである。

結論：以下のような数表を下から上に見ていけばよい。n = 1234567890 であっても，高々これだけの計算をしてやればよいだけ。

            x         y
43 1134903170 701408733
42  701408733 433494437
41  433494437 267914296
40  267914296 165580141
39  165580141 102334155
38  102334155  63245986
37   63245986  39088169
36   39088169  24157817
35   24157817  14930352
34   14930352   9227465
33    9227465   5702887
32    5702887   3524578
31    3524578   2178309
30    2178309   1346269
29    1346269    832040
28     832040    514229
27     514229    317811
26     317811    196418
25     196418    121393
24     121393     75025
23      75025     46368
22      46368     28657
21      28657     17711
20      17711     10946
19      10946      6765
18       6765      4181
17       4181      2584
16       2584      1597
15       1597       987
14        987       610
13        610       377
12        377       233
11        233       144
10        144        89
9          89        55
8          55        34
7          34        21
6          21        13
5          13         8
4           8         5
3           5         3
2           3         2
1           2         1

フィボナッチ数列の各項下3桁のみからなる数列の一般項

a[0]=0
a[1]=1
a[i]=(a[i-1]+a[i-2]) mod 1000, i ≧ 2

素直に計算しても答は簡単に求まる。

しかし，各項は高々 3 桁なのだから，m 項が 0 で，m+1 項が 1 になることもあるだろうと...
実際に調べれば，m = 1500 とわかる。
つまり一般項 a[n] は，a[n] = a[n mod 1500] ということ。
素直に考えるだけじゃダメという訳か。

コラッツの問題（2）

単純に，10 進数一桁を要素とするベクトルを使って，掛け算も，割り算も，自前でやるプログラムを書く。10 進数は，1 の位が添え字 1 になるように（逆順）にすると，プログラムが書きやすい。

途中経過をプリントするのを含めて，余裕の 24 行だ。

n = rep(9, 50)
print(sub("^0*", "", paste(rev(n), collapse="")))
repeat {
  if (n[1] %% 2 == 1) {
    n = 3 * n
    n[1] = n[1] + 1
    carry = 0
    for (i in seq_along(n)) {
      n[i] = n[i] + carry
      carry = n[i] %/% 10
      n[i] = n[i] %% 10
    }
  } else {
    borrow = 0
    for (i in rev(seq_along(n))) {
      n[i] = borrow * 10 + n[i]
      borrow = n[i] %% 2 == 1
      n[i] = n[i] %/% 2
    }
  }
  string = sub("^0*", "", paste(rev(n), collapse=""))
  print(string)
  if (string == "1") break
}