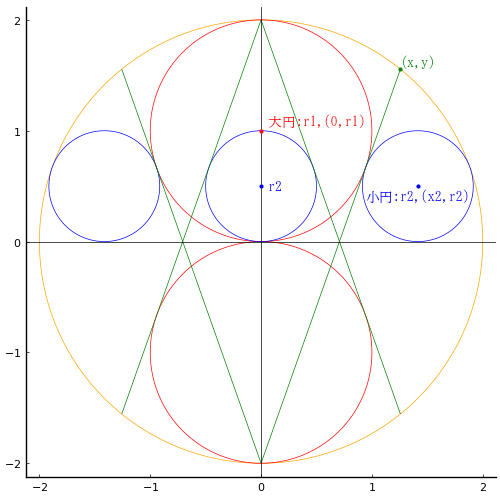算額（その557）

算額（その557）

群馬の算額 104-2 長谷寺 文久元年
http://takasakiwasan.web.fc2.com/gunnsann/g104-2.html

3 個の正三角形と大円，小円が図のように配置されている。正三角形の一辺の長さが与えられたとき，小円の直径を求めよ。

正三角形の一辺の長さを a とする。
大円の半径と中心座標を r1, (0, √3a/2); r1 = a/2
小円の半径と中心座標を r2, (0, √3a/2 - r1 + r2)
とおき，方程式を解く。

include("julia-source.txt");

using SymPy

@syms r1, r2, a

r1 = a/2
eq = r2/(r1 - r2) - 1//2
solve(eq, r2)[1] |> println

   a/6

小円の半径は正三角形一辺の長さの 1/6 である。
小円の直径は正三角形一辺の長さの 1/3 である。

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   a = 1
   r1 = a/2
   r2 = r1/3
   @printf("小円の直径 = %g;  r1 = %g;  r2 = %g\n", 2r2, r1, r2)
   plot([a, 0, a, 2a, a, 0, -a, -2a, -a, 0, -a] ./ 2, [0, 0, √3a, 0, 0, √3a, 0, 0, √3a, 0, 0] ./ 2, color=:blue, lw=0.5)
   circle(0, √3a/2, a/2, :orange)
   circle(0, √3a/2 - r1 + r2, r2, :red)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:black, lw=0.5)
       vline!([0], color=:black, lw=0.5)
       point(0, √3a/2, " √3a/2", :black, :left, :vcenter)
       point(0, √3a/2 - r1 + r2, " √3a/2-r1+r2", :black, :left, :vcenter)
       point(0, √3a/2 - r1, " √3a/2-r1", :black, :center, delta=-delta/2)
   end
end;

算額（その556）

算額（その556）

群馬の算額 104-1 長谷寺 文久元年
http://takasakiwasan.web.fc2.com/gunnsann/g104-1.html

外円内に弦を引き，区画された領域に大円 2 個，小円 3 個を入れる。大円の直径が与えられたとき，小円の直径を求めよ。

大円の半径と中心座標を r1, (0, r1)
小円の半径と中心座標を r2, (0, r2), (x2, r2)
斜めの弦と円の交点座標を (x, y)
とおき，方程式を解く。

include("julia-source.txt");

using SymPy

@syms R, r1, r2, x2, x

R = 2r1
eq1 = (R - r2)/(2R - r1) - r2/r1
eq2 = x2^2 + r2^2 - (R - r2)^2
eq3 = x/sqrt(x^2 + (2r1 + sqrt(R^2 - x^2))^2) - r2/(R - r2)
solve([eq1, eq2, eq3], (r2, x2, x))

   2-element Vector{Tuple{Sym, Sym, Sym}}:
    (r1/2, -sqrt(2)*r1, 8*sqrt(2)*r1/9)
    (r1/2, sqrt(2)*r1, 8*sqrt(2)*r1/9)

2 組の解が得られるが，2 番目の解が適解である。

小円の半径は大円の半径の 1/2 である。
また，外円の半径は大円の半径の 2 倍である。

その他のパラメータは以下の通り。

   小円の直径 = 1;  r1 = 1;  r2 = 0.5;  x2 = 1.41421;  x = 1.25708;  y = 1.55556

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   r1 = 1
   R = 2r1
   (r2, x2, x) = (r1/2, sqrt(2)*r1, 8*sqrt(2)*r1/9)
   y = sqrt(R^2 - x^2)
   @printf("小円の直径 = %g;  r1 = %g;  r2 = %g;  x2 = %g;  x = %g;  y = %g\n", 2r2, r1, r2, x2, x, y)
   plot()
   circle(0, 0, R, :orange)
   circle(0, r1, r1)
   circle(0, -r1, r1)
   circle(0, r2, r2, :blue)
   circle(x2, r2, r2, :blue)
   circle(-x2, r2, r2, :blue)
   plot!([-x, 0, x], [-y, R, -y], color=:green, lw=0.5)
   plot!([-x, 0, x], [y, -R, y], color=:green, lw=0.5)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:black, lw=0.5)
       vline!([0], color=:black, lw=0.5)
       point(0, r1, " 大円:r1,(0,r1)", :red, :left, :bottom, delta=delta/2)
       point(0, r2, " r2", :blue, :left, :vcenter)
       point(x2, r2, "小円:r2,(x2,r2)", :blue, :center, delta=-delta/2)
       point(x, y, "(x,y)", :green, :left, :bottom)
   end
end;

 

算額（その555）

算額（その555）

群馬の算額 104-5 長谷寺 文久元年
http://takasakiwasan.web.fc2.com/gunnsann/g104-5.html

3 個の大円が交差しており隙間に中円，小円を入れる。大円の直径が与えられたときに小円の直径を求めよ。

方程式の構成に必要な円のみ
大円の半径と中心座標を r1, (0, 0)
中円の半径と中心座標を r2, (r2, 0); r2 = r1/2
小円の半径と中心座標を r3, (x3, y3); x3 = r2, y3 = r2 + r3
とおき，方程式を解く。

include("julia-source.txt");

using SymPy

@syms r1, r2, r3, y3

r2 = r1/2
x3 = r2
y3 = r2 + r3
eq1 = x3^2 + y3^2 - (r1 - r3)^2
res = solve(eq1, r3)[1]
res |> println

   r1/6

小円の半径は大円の半径の 1/6 である。

その他のパラメータは以下の通り。

   小円の直径 = 0.333333;  r1 = 1;  r2 = 0.5;  r3 = 0.166667;  y3 = 0.666667

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   r1 = 1
   r2 = r1/2
   r3 = r1/6
   x3 = r2
   y3 = r2 + r3
   @printf("小円の直径 = %g;  r1 = %g;  r2 = %g;  r3 = %g;  y3 = %g\n", 2r3, r1, r2, r3, y3)
   plot()
   circle(0, 0, r1)
   circle(r1, 0, r1)
   circle(-r1, 0, r1)
   circle(r2, 0, r2, :orange)
   circle(3r2, 0, r2, :orange)
   circle(-r2, 0, r2, :orange)
   circle(-3r2, 0, r2, :orange)
   circle4(x3, y3, r3, :blue)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:black, lw=0.5)
       vline!([0], color=:black, lw=0.5)
       point(r1, 0, "r1 ", :red, :right, :bottom, delta=delta)
       point(r2, 0, "r2", :orange, :center, :bottom, delta=delta)
       point(x3, y3, " 小円:r3,(x3,y3)", :blue, :left, :vcenter)
   end
end;