マミさんの愛した数式①：虚数から複素平面へ

梅雨のわずかな晴れ間、キュウべえが巴マミのところへやって来た。
「あら、ひさしぶり。お茶でも飲む？」
「いや、遠慮しておくよ。…君は今は大学で物理を勉強しながら、数学の講師をしているそうだね」
「高校生相手の小さな塾でね。数学なのか算数なのかはわからないけど」
「じゃあ、この式は知ってるよね」

「ええ、オイラーの等式ね。つまんない小説や映画で有名になったけれど」
「つまんないか。…そうすると君はこの式の意味をわかっているのかな？」
「わかっているんでしょうね。十分かどうかは自信ないけど。…どうしてこれに興味を持ったの？あなたたちの文明なら小学校で習ったりするんじゃないの」
「そうでもないんだ。数学はコンピュータに任せておけばいいという考えが支配的でね。…ところが、この星の人間たちは数学を好きとか嫌いだとか、果ては美しいとか愛してるとか。全く理解できないよ」
「うふふ、それで知りたくなったの？」
「そうなんだ。巴マミ、ぼくと契約してこの数式の意味を教えてよ！」
「契約なんかしなくても教えてあげるわよ。殺されちゃかなわないわ」
「じゃあ、とびきりおいしいマカロンをあげるよ」

「その方がいいわね。…どこから始めようかしら。キュウべえの数学の知識はどれくらいなの？」
「君たちの授業を聞いてただけだから、中学の数学だけだね」
「あらら、それは大変。テーラー展開とかロンスキー行列なんかを使っちゃ無理ね」
「そういうのは説明になってないよ。本当はわかってないのをごまかしてるだけじゃないのかな」
「ふうん、一応は調べたのね。…虚数単位ｉの意味はわかってる？虚数：imaginary numberの頭文字だけど」
「２乗してー１になる数でしょ。暁美ほむらが『虚数を用いればＸ^2＝－１にも解はあります』って早乙女先生を困らせてたから」
「ふふ、あの子らしいわね。じゃあ、始めるわ。…１に－１を掛けると？」
「－１でしょ」
「もう１回－１を掛けると？」
「１に戻るね」
数直線を書いて、１と－１が原点０を挟んで行ったり来たりする図を描く。
「こんな感じね。今度はｉを掛けていきましょ。１×ｉは？」
「ｉだね」
「それにまたｉを掛けると？」
「－１だね。…ははーん」
「わかってきたみたいね。３回掛けると？」
「－ｉ。もう１回掛けて、４回目で元の１に戻るわけか」
「そう、それを図で描くとこうなるわけ。この複素平面を使えば実数＋虚数の複素数（complex number）が表わせるんだけど」

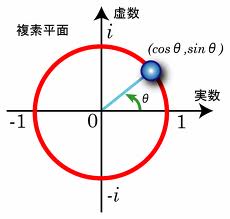
「なるほど。ｉを掛けるっていう操作を90度回す操作と見ているわけか」
「そうだけど、ラジアンでπ/2と言ってほしいわね」
「ラジアンってなんだい？」
「角度の呼び方。…１の長さの棒でどれだけ棒の先が掃いたかってことよ」
「ん？…１の長さでぐるっと１周、円を描けばその長さは２π。その1/4の直角はπ/2か」
「うんうん。そうすると－１がπになるでしょ」
「ほほー、ｉからもう－１とπの関係が見えてきたね。簡単じゃないか」
「それがそうでもないのよ。ここからが面倒なの」
「そうなの？…オイラーの等式のπの部分を角度の変数だと見て、この円を表わした関数が式の左辺ってことでいいんじゃないか？」
「全くそのとおりよ」

「この式は複素平面における極座標形式での単位円の方程式を左辺は自然対数の底ｅによる指数関数を、右辺は三角関数をそれぞれ用いて表わしたものよ。これがオイラーの公式なの」
「…いきなりフィロ・フィナーレをぶちかましたね。さすがについていけない。もうちょっと話を聴くよ」