黄金比じゃなくても自然は成長する

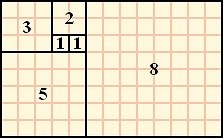
　前回は植物について見たので、今回は動物から見ていきます。上の画像は第２回目にも出したもので、フィボナッチ数列を１辺とした正方形がきちんと並べていくことができるのを示しています（もうちょっと数学的な意味はそのときに説明してあります）。また、順にできていく長方形のたて・よこの比率はフィボナッチ数列の隣接項の比率ですから、黄金比φ＝(1+√5)/2≒1.6180339887に近づいていき、この図でも既に13／8＝1.625になっています。ですので、これを黄金長方形と呼んだりするみたいです。で、この図をもっと続けていってそれぞれの正方形の中に1／4の円を描いていくと次のようになります。



　きれいならせん（スパイラル）が現われましたね。黄金比を求める連分数を思い出させるものがあります。これと次のようなオウムガイの断面図を見ると「おおー、同じだ」って思いません？



　ほとんどの書物やサイトでは、これを黄金比が動物に現われた典型例としていますし、常識に近いようになっている気さえします。見た目だとオウムガイの方が広がりがちょっと小さいかもしれないけど、縮尺を変えれば重なるんじゃないかって。……黄金比とフィボナッチ数列について魅力的な本を書いたマリオ・リヴィオですら同じものだと思っているようです。しかし、これはこのとても行き届いたサイトを見るとあまりにもおおざっぱな議論だということがわかります。それを参考にして説明したいと思います。

　まず、黄金長方形のらせんを書こうとすると90度ごとにコンパスの中心を移動し、フィボナッチ数列の次の項の数値に合わせていくことになりますね？　ということは、このらせん（カッコよく黄金スパイラルと呼びましょう）は90度回転するたびに(1+√5)/2倍に広がっていくという性質をもっています。最初の方はそうならないじゃないかって？　いい質問です（自分で考えたんですからｗ）。もともと1/4の円を描いていくというのは黄金スパイラルの近似的な書き方なんです。実際には次のような式で定義されるなめらかな曲線の１種です。



　これだけでサブイボが出そうな人もいると思いますが、これは通常のx-y座標（直交座標）ではなく、中心からの距離rと角度θで表わされた極座標による表現です。てなことを言うとむずかしそうですけど、50メートル、北東（右斜め45度）に向かって歩けっていうことと同じです。ミサイルなんか発射するときは３次元ですから、仰角を入れた球面座標ってものを使うんだろうと思います。あの国に訊いたわけじゃありませんがｗ。この極座標は丸っこい図形を式で表現するときに威力を発揮します。中心が原点（０,０）にある円の方程式は、学校では次のようなうんざりするようなものを教えましたね。

　　x^2＋y^2＝a^2　（aは半径、^2は２乗を表わし、片目で笑って耳を引っ張っているのではない）

　ところが極座標では、

　　r＝a

　これだけです。だって角度θに関係なく、原点から同じ距離の点の集合が円ですから。次に蚊取り線香やロープを巻いたらせんの式と図は次のようになります。

　　r＝aθ



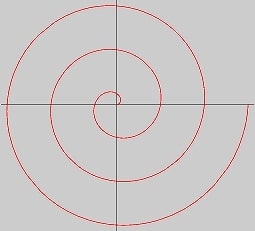
　これはアルキメデスのらせんっていうそうですが、名前なんかどうでもいいです。要は間隔が一定で１回転したときに２倍、もう１回転すれば３倍……となるものだってことです（a＝1／360とすればわかりやすいかもしれません）。だからこのらせんは拡大・縮小すればすべて重なるわけで、相似、もっと簡単な言葉で言えば同じ形をしています。円や正方形がそうであるように。
　
　さて、さっきのサブイボの方程式ですが、これは対数らせんとか等角らせんっていいます（このらせんを深く愛した数学者の名前をとってベルヌイらせんとも言います）。対数らせんって呼ぶのは、さっきの式を自然対数lnを使ってθについて解くと、
　
　θ＝1/(cotb)ln(r/a)

となるからなんですね。まあ倍々ゲーム、指数関数的に広がっていくらせんをイメージしていただければいいと思います。



　等角らせんって呼ぶのは、この図のように中心から引いた線とそこに接線を書いてできる角度が一定だからです。で、その角度がbでそのコタンジェント、tanの逆数が式に出てきて、このらせんの広がり具合を決定しているんです。でも、なぜcotが出てくるのか、そもそもなぜ角度が一定になるのかについて、サイトはもちろん、いろんな数学の本や辞書を調べましたが、どれもこれも同じような（はっきり言ってしまえば敷き写しの）記述ばかりで何にもわかりませんでした。だいいちcotすら出て来ないものが多いし。……

　私のような素人の素朴な質問に答えてくれたのは結局、前回もお世話になった英語のサイトです。もう一般の書店や図書館で数学についてあれこれ調べる気はなくなりました。……まあ、このサイトにたどりつくまでに自然対数の底eについての微分の公式なんかを見ながら自分でやってみて、だいたいは見当がついてたんですが、極座標は初体験ｗだからどうも自信がなくて。

　それはさておき、対数らせんでは角度bが違えばいくら拡大・縮小しても重なりません。係数aはアルキメデスのらせんと同じく縮尺のようなものですから、どんな数でもいいんですが。……黄金スパイラルとオウムガイではこの角度が違うんですね。では、黄金スパイラルの角度bは何度か？　まず、対数らせんの方程式のθによるものを使ってcotbについて解きます（aは本質的な要素ではないので、１とします）。

　　cotb＝(1/θ)ln(r)

　この式で、θが90度（ラジアンではπ/2）回るごとにφ＝(1+√5)/2ずつ拡大するわけですから、

　　cotb＝(2/π)ln(φ)

　右の数値になるbを求めればいいんで、cotの逆関数（アークコタンジェントと言い、英語のサイトの(4)の式に出てきたcot^-1は－１乗でも、片目をつぶって…＜もういいってｗ、でもなく、これのことです）ってことになります。グーグルの電卓機能（πもφも定数で入っているので便利です）を使います。

　　「arccotangent((2 / π) * ln(phi)) を度で」＝72.9676089 度

　一方、最初に紹介したサイトによるとオウムガイにおけるbは80度くらいだそうです。ずいぶん違うでしょ？……え？　７度くらいの差なんて誤差の範囲内じゃないかって？　そ、そうかな。でも、90度回転するとこっちは何倍になるかって言うと、サブイボの式を使って、

　　「exp(cotangent（80度）*π/2」＝1.31913177倍ですよ。

　え？　1.6180339887倍とじゃやっぱりあんまりかわんないって？　じゃあ、１周、360度（＝2π、円を１周回ったときの距離です。ラジアンって極座標的です）回るとどうなるか。

　　「exp(cotangent(80度) * 2π)＝3.02797807」ですが、

　　「exp(cotangent(72.9676089度) * 2π)＝6.85410194」

　で、大違いです。どう縮尺を調整してもぜったいに重ならず、どんどんずれていきます。これが指数関数のこわいところです。ご利用は計画的にｗ。……まあ、楕円や長方形がいろいろあるのと同じようなもんで、オウムガイに黄金比があると言う人は適当な長方形を見て、縦横が黄金比だと言っているのと変わんないですね。

　そんなことよりも重要なのは、動物の世界で立体に拡大された対数らせんが見られることです。巻貝や羊の角にも……オウムガイの断面図をもう一度見てください。小さな部屋がだんだん大きくなっていくのがわかりますね。体が大きくなったのに合わせて部屋を大きくしていったんでしょう。成長し、膨張するものの例として、台風と星雲（猟犬座M51星雲、子持ち星雲として有名なものです）の写真を掲げます。





　こういうのを見ると生物ではないのに生命力のようなものを感じるのは私だけでしょうか。ベルヌイは変化しながら変わらない対数らせんに不死を見ていたようです。