「ちょっと話を整理しましょう。…ふつう学校でならう座標はAという点を(x,y)で表わすわよね。北緯35度、東経135度みたいに」
「うん、そうだね」
「これを直交座標っていうの。でも、原点からAに向かっての角度と距離で表わすこともできるでしょ。ここから見滝原中学校は真東から30度の方向に2キロみたいに」
「その方が便利だし、わかりやすいね。10時の方向に敵機発見、距離約4キロとか」
「それが極座標なの。Aまでの距離をr、x軸からの角度をθとすると(r,θ)で表わせるわけ」
「うん、それで?」
「x軸をふつうの数直線、実数軸とし、y軸をiの実数倍、虚軸とすると複素数a+ibが(a,b)で表わせるの」
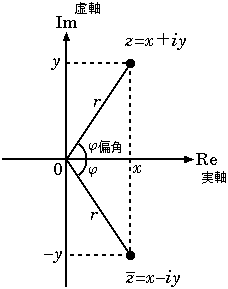
「たてよこで押さえてるから直交形式か。…2つの実数の組み合わせが1つの複素数になる。つまり複素数を使えばベクトルを簡単に表現できるのかな」
「ええ、電気の分野で複素数が使われるのもそういうことなの。ってなんでベクトルのこと知ってるの?」
「不思議なことを言うね。重さや分量のことは学校で習わなくてもわかっているだろう?それと同じじゃないか」
「a+ibという複素数が極座標で(r,θ)と表わせたとすると、
a=rcosθ ;b=rsinθとなるわけ。これが極形式」
「何?そのサインとかコサインって」
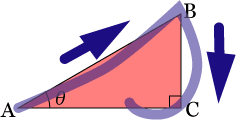
サインの覚え方ね。

コサインはこう。
「直角三角形の辺の比を角度を用いて表わしたものってこと」
「ふうん。直角三角形の形は角度で決まるからね…えっとこことここの比にrを掛ければ実数部分の長さaになるの当たり前じゃない」
「数学っていうのは当たり前を積み重ねただけ。国による違いなんかないのよ」
「なるほどね」
「で、r=1の円を単位円っていうんだけど、そうするとオイラーの公式の右辺:cosθ+isinθは単位円上の点の表現ってことなの」
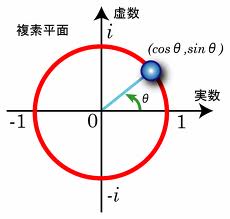
「うん、わかったよ。θ=πならcosπ=-1、isinπ=i×0=0で-1だね」
「それだと神秘的でもなんでもないけどね」
「うん、そうだね」
「これを直交座標っていうの。でも、原点からAに向かっての角度と距離で表わすこともできるでしょ。ここから見滝原中学校は真東から30度の方向に2キロみたいに」
「その方が便利だし、わかりやすいね。10時の方向に敵機発見、距離約4キロとか」
「それが極座標なの。Aまでの距離をr、x軸からの角度をθとすると(r,θ)で表わせるわけ」
「うん、それで?」
「x軸をふつうの数直線、実数軸とし、y軸をiの実数倍、虚軸とすると複素数a+ibが(a,b)で表わせるの」

「たてよこで押さえてるから直交形式か。…2つの実数の組み合わせが1つの複素数になる。つまり複素数を使えばベクトルを簡単に表現できるのかな」
「ええ、電気の分野で複素数が使われるのもそういうことなの。ってなんでベクトルのこと知ってるの?」
「不思議なことを言うね。重さや分量のことは学校で習わなくてもわかっているだろう?それと同じじゃないか」
「a+ibという複素数が極座標で(r,θ)と表わせたとすると、
a=rcosθ ;b=rsinθとなるわけ。これが極形式」
「何?そのサインとかコサインって」

サインの覚え方ね。

コサインはこう。
「直角三角形の辺の比を角度を用いて表わしたものってこと」
「ふうん。直角三角形の形は角度で決まるからね…えっとこことここの比にrを掛ければ実数部分の長さaになるの当たり前じゃない」
「数学っていうのは当たり前を積み重ねただけ。国による違いなんかないのよ」
「なるほどね」
「で、r=1の円を単位円っていうんだけど、そうするとオイラーの公式の右辺:cosθ+isinθは単位円上の点の表現ってことなの」

「うん、わかったよ。θ=πならcosπ=-1、isinπ=i×0=0で-1だね」
「それだと神秘的でもなんでもないけどね」