
どうも前回の「役に立たない勉強」へのコメントを拝見していると、誤解されるような書き方、特に表題がよくなかったかなと反省しています。私は数学が論理的思考を養うのに役立つと思っていますし、本当は(人工言語でかつ修飾語のない数式で記述されることなどから)数学は厳密にものを考えるのに不可欠だと思っています。また、科学の成果を(一般向けの啓蒙書などによらず)自分で確かめようとすれば大学初級程度の数学の知識は不可欠です。
言いたかったのは、数学のそうした必要性、役に立つことがきちんと学生を始めとしたふつうの人たちに説明されていないということと、数学教育(算数教育ではありません!)を無用又は懐疑的に見る人たちの方が優勢なのではないかということです。つまり数学教育が「強制」されているから、意趣返しを受けているのではないか、“すっぱい葡萄”のような扱いを受けていると感じたのです。
でも、もし私の考えが誤解されていたとしても、無視されるより何倍もいいことだと思いますし、こうやって前回の二つの論点についての私の考えをストレートに述べることができたので、感謝申し上げたいと思います。
さて、今回は論点のうちの一つめをもう少し掘り下げたいと思います。数学がなぜ論理的思考に役立つのか、その根本的な理由は何かということです(二つめの数学の科学への応用や寄与については、今さら論じる必要はないでしょう)。この問題を考えるには、用語の定義とか中間的に整理、検討しておくべきことはいろいろあると思いますが、ぜーんぶすっ飛ばしてw、結論だけ言ってしまうと、3つくらいの立場にわかれるように思います。
①「論理的思考」とは「数学による思考」に他ならないので、役立つのは当たり前と言うか、トートロジーであるという立場。「数学による思考」を例えば「記号論理学」に置き換えればわかりやすいかも知れません。
②数学の論理の進め方と人間の脳の論理的思考を司る機能が同じだからだという立場。
③数学的論理構造が(人間の脳を含めて)この世界の構造そのものを表わしたものだからだという立場。
このうち、①は正しいかどうか以前に何の生産性もない不毛な議論でしょうし、論理的な思考と数学的思考が近しい関係にあるのは、古代ギリシアと現代くらいだという歴史的事実を無視しています。例えばインドや中国の仏教哲学や儒教、イスラム哲学は数学とは無関係に高度な発展を果たしてきたからです(そうした過去の哲学思想が記号論理学のようなものに還元あるいは翻訳できると主張するのであれば、ちゃんと原典を読んだの?って言うしかありません)。逆に江戸時代に高度なレヴェルまで発展した和算は、同時代の儒学における論理的思考の発達(荻生徂徠などなど)と比べると論理的展開力に乏しいのです。つまり現在では考古学的関心の対象にしかならないのです。
次に②は、まあいちばん無難な解答だと思われます。脳の機能の一部を数学として切り出したのだから、原理的に同じになっているに決まっていると言えばもっとわかりやすいかも知れません。「脳機能→数学」という写像なのだからというわけです。
これを否定することはむずかしいですし、やめておいたほうがいいと思いますが、一つだけ指摘しておきたいのは、チューリングマシンのことです。チューリングマシンには有限回で停止することができない命題が存在し、かつある命題が有限回で停止するかどうかを事前に判断することが不可能であることをチューリング自身が証明しました(そしてこれはゲーデルの「不完全性定理」と同値であると言われています)が、このことは今の文脈でどう理解されるのかということです。
「脳機能→数学→チューリングマシン」であるならば、おおもとの脳自体に堂々巡りになっていつまで経っても(この宇宙が終わっても)解決できないことがあって、しかも堂々巡りになることを予防できないということなりますw。そんなのよくあることじゃないのって思うでしょ? でも、数学で起きるなんて……論理的思考を追求して行った先は、こういうことになってるんですよね。
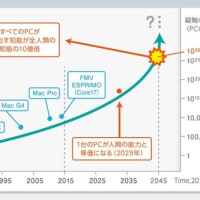
なお、チューリングマシンは現在のコンピュータの基本機能を(私の理解では)あますところなく描写していますので、「脳機能→数学→チューリングマシン→コンピュータ」という写像が成り立ちます。ここで、「数学→チューリングマシン」が全射なのか、すなわちチューリングマシンに数学がすべて還元されるのかは、私の乏しい知識では答えられません。また、「チューリングマシン→コンピュータ」が全射なのか、すなわち今後開発されるコンピュータあるいはAIが原理的にチューリングマシン以外のものとなりうるのかは、「脳機能→コンピュータ(AI)」が全射になりうるのかという問題との関連でも、非常に興味のあるところです。
③ですが、数学によってこの世界の構造、平たく言えばどういうものなのかがわかるって言ってるわけですから、これはまず非常識です。だから私は好きですw。中学とか高校の授業で教師が言ったら、嘲笑されてしまうでしょうけど。世界の構造なるものが示されない以上、証明は不可能、って言うかぁ信念、信仰みたいなものですからね。でも、数学者の頭の中にはかなり根強くあるようで、特に応用数学でなくて数論のような基礎数学の分野では多いみたいです(博士の愛した数式かな?w)。
これは、あっさり言ってしまえばいわゆるイデア論に基づく発想で、現実世界を超えたイデアが真の実在であるという考えですからプラトニズムです(日本の数学者は哲学の知識が十分ではないようにも思いますが)。ただ急いで言っておくと、プラトンの「国家」を始めとした著作といわゆるイデア論やプラトニズムとは違ったものと考えた方がいいと思います。プラトンの展開している議論はそうそう簡単な要約を許すようなものではありませんし、例えば今の議論とはぜんぜん違う分野ですが、カール・ポパーの有名な「オープン・ソサエティとその敵」などはプラトンの著作をまじめに読んだとは思えない代物、自分の主張のダシにプラトンを使っているだけだからです。
それはさておき、フェルマーの最終定理についての本を読んでいて、特に谷村・志村予想(ワイルズの証明はこの予想の一部を証明する形で行われたのですが)を知ったときには、この世界の構造を把握する、宇宙をまたぐ壮大な架け橋を見たような思いにとらわれました。確かにああいう研究をしていると、神の設計図を垣間見るような気持ちになることもわかるような気がします。多くの数学者が敬虔な信者になるのは、当然なのかも知れません。
さて、数学が役に立つかどうかから出発しながら、ずいぶん実生活から離れたところまで来てしまったようです。でも、本当の意味でものごとを考えている人の考えは数学者に限らず、ふつうの人が生ぬるい感覚でおしゃべりしているものとは何にも関係はないのです。



















「自己言及命題と無限集合が深刻なパラドックスを引き起こして、不完全性定理が生まれた」とHPにも載せている物語の(4)朝はカクテルを飲まない の中で、主人公に言わせていますw。
>「一つの≪系≫の完全性をその≪系の内部≫では証明できない」と考えると、トートロジーに至る…
それが結論ということではないんですが、結論を出していない点では変わらないです。
>分析と総合を往還するのも抽象と具象を往還するのもヒトに≪純粋経験≫が不可能
いわゆる「イデア」は、経験や物質に先立って「ある」ものなので、経験や物質の後にくる抽象とか概念とは違うものなんです。それを知るためには哲学的訓練が必要だとされているんですが。
アリストテレスやデカルト、カントなどの近代哲学の用語でプラトンを理解するのは、適当ではないと思います。
自然科学は還元主義的に納得しますね。そこで「マシーン」にひきづられて≪観測の限界≫を言いたかったんです(笑)。その先は数学ですね。
プラトンの≪イデア≫もデカルトの≪合理主義=人間至上主義≫もミスリードの産物でしょう(笑)。それはプラトンが神学に影響を与えて、神学が人間原理を準備して…と、現在時点から過去を再構成するしかない原理的な弱点ですね。分析と総合を往還するのも抽象と具象を往還するのもヒトに≪純粋経験≫が不可能だからしかたがないわけで、しかし、意味のズレやズラシが新たなものを生み出してきたことも事実のように思います。いや、その意味が捕捉できないからズレて見えているだけなのか(笑)。
私は、ここでは数学が論理的思考に役立つかどうかを論じているのではなく、なぜ役立つのか、その根本的理由を考えてみたかったのです。
その点についての8マンさんのお考えはよくわからないですが、③のプラトニズムではないようですね。でも、本文にも書きましたけど、数学者にはこういう立場を取る人が多く、例えば我が国の代表的なグラフ理論学者の根上生也先生のHPを見ると、まあ(哲学的には)素朴なプラトニストです、ご本人がどう思っているかは知りませんがw。
ハイゼンベルクの不確定性原理は「客観性」を否定していますが、ゲーデルの不完全性定理は「完全に合理的な体系の否定」を主張しています。時代思潮としては相通じるものがあるのですが、やはり違うものでしょう。
プラトニズムの価値が既存価値の転倒にあるというのは、正しいと思います。まあ、デカルトとともに近代の基礎を与えたというご主張もそうかなぁとも思います。でも、プラトンの思想はそんな枠に納まるものではないとも思います。
③などは、まさに唯心論で、面白いですね。でも、脳の機能の概念構成を写し取ったかの如き集合論に照らし合わせて即刻却下ではないですか(笑)。チューリングマシンのことはよくわからないのですが、還元的な証明の根拠はハイゼンベルグの不確定性原理でも同相だと思います。
プラトニズムは価値の転倒にこそ価値があるのだと思います。逆照射されて見えてくる暫定的な真理もあるでしょ、というわけです。結局のところ、プラトンとデカルトを経て、西洋の近代は意気揚々と立ち上がったわけでしょう? 限界はあるにせよ、お役立ちでした。もちろん≪系≫それ自体の完結的なエレガンスを否定するつもりは毛頭ありません(笑)。
リーマンとオイラーは人間業と思えないほど広い分野の研究を行っていて、彼らの業績を追うとおっしゃるような意味がよくわかります。
「最近、数学の効用は何かと尋ねられて、『数論は暗号の作成に役立つ』というような答えをする人がいる。それは、『音楽は映画演出に使われるから効用があるのだ』というようなもので、ばかげた答えだ。音楽は映画と無関係に効用があるように、数学も、それ自体に価値がある。それは、人の精神や思索を豊かにするという効用なのだ」
まあ、そういうことだと思います。
今になってぼちぼち数学そのものの本を読んで楽しんでいます。
トラックバックしていただきありがとうございます。
ネタが数学という事(?)で・・・
少々戸惑いを感じていますが
脳機能やアラン・チューリングの
「チューリング・マシ~ン」も上がっていましたので
良しとして。
数学に関しては如何せんダメで、
学生時代にはズバ抜けて成績が悪い。
しかし数学が嫌いなわけではなく
寧ろ、大変興味があり
ここ二年くらいは「数学教えて」が口癖です。
近々中学1年生の数学からやり直すつもりでおり
ドリルでも買ってガチガチにやってみようかと。
ひとまずは高校の数学までやり、その後は分数の
足し算、引き算、掛け算、割り算と進めていこうと
思う次第です。はい。
数学好きですが、中高の授業は嫌で嫌で。
何かにつけ受験のことしか言いませんから。
ただ、授業後に個人的に先生方に難問を
ぶつけては解法を教えてもらってました。
これは楽しかったのを今でも覚えています。
既にこの頃から思考がズレてたようです:)
論理的思考は、事象のパーツ分解のルールを
決めることに近いのではないかと思います。
ある事象があって外面からしか見れないとして
その内部をどう分解して構成できるかです。
切り方が事象によってマチマチでは、それらの
事象の内面を比較したり考察したりすることが
困難となります。分解の仕方が中途半端だと
どれとどれが比較できるのかあやふやです。
微細な世界まで分解すればするほど、世界
そのものの構成にまで辿り付けます。しかし、
普通の人間だと全てをその分解ルールに則り
事細かく分解していくことは困難でしょう。
論理的思考を学ぶ意味は、このルールの
揺らぎを低減し、各事象をなるべく等しく
認知比較できる意識を持つことです。これを
「ものさし」としてみれば、数学的思考が
道具である面が見て取れます。
と、書きながら僕の頭の中では、果物を
ナイフで切り分ける図が浮かんでおります。
やはく帰宅して夕飯食べようと思います:)
とりあえずそれだけです。
ただ、あんまり行き過ぎると神秘思想みたいになるんでしょうし、そのちょっと手前くらいが好きですね。
Wolframって、セル・オートマトンの人でしょうか?
今後ともよろしくお願いします。
私個人としては、別に「論理的思考を養うには数学でなければならない」なんて思わないし、ましてや数理的構造が世界を表しているなんて言う気は起きません。ただ、道具としては有用だし、将来の選択肢を広げる為にも学校で教える意味はあるかと。
どこぞやでWolframが「数学が世界の構造を研究するのに有用なのは、数理的構造がそれらを作り出しているからではなく、数理的構造と同じような過程で構成されているからだ」みたいな主張をしていました。冊子の最初の2ページくらいしか読んでいませんが(爆)。まあ、そのような考え方もあるということで。