円周上に並んでいる個体を 1 個ずつ取り除いて...

1～2*n 番目までの 2*n 個の個体が円周上に並んでいる。2 番目から初めて 1 つ置きに取り去る。最後に取り除かれるのが最初に並んだときの n 番目の個体であるような n を小さい方から 5 つ求めよ。

k = 0
n = 5 # 21, 85, 341, 1365, 5461, 21845       i.e. a[1]=5, a[i]=4*a[i-1]+1, i > 1
repeat {
  n = n+1
  seat = logical(2*n)
  seat[n] = TRUE
  i = 2
  ok = TRUE
  for (m in (2*n-1):1) {
    if (seat[i]) {
      ok = FALSE
      break
    }
    seat
    i = i+1
    if (i > m) i = i-m
  }
  if (ok && seat) {
    print(n)
    k = k+1
    if (k == 5) break
  }
}

このプログラムで 4 つ目までは比較的短時間で求まる。最初の n=5 を含めて，よく眺めると，規則性があることが分かる。で，5 つ目は 5461 であると当たりを付けて計算してみると確かに n = 5461 は解である。21845 は 6 つ目...

証明ができればよいのだけど。

漸化式が知られている

> 12人全員が他人のパソコンを持って帰ってしまうような組み合わせが何通りあるか

Wikipedia 曰く，

完全順列（かんぜんじゅんれつ、英 Derangement）、もしくは攪乱順列（かくらんじゅんれつ）とは、整数 1, 2, 3, …, n を要素とする順列において、i 番目 (i ≤ n) が i でない順列である。

完全順列の総数はモンモール数という。

モンモール数 a_n を与える漸化式は a_n = (n-1)(a_n-1+a_n-2), n ≧ 3

a₁ = 0, a₂ = 1

> an = function(n) {
+     if (n == 1) {
+         return(0)
+     } else if (n == 2) {
+         return(1)
+     } else {
+         return((n-1)*(Recall(n-1)+Recall(n-2)))
+     }
+ }

> an(3)
[1] 2

> an(4)
[1] 9

> an(12)
[1] 176214841

変わった数の二乗

9 桁の整数を二乗して，結果の下 9 桁が最初の数と同じになる。そういう数を見つけなさいと...

素直にやっていくとどうしようもない。どうせ，各桁の取り得る値は限られているのだから，下の桁から可能性を絞っていくという戦略で，ループを段階的に深くしたプログラムにしていく。問題は 9 桁の数の二乗は倍精度実数でも整数として表現しきれない場合があるということ。最初から gmp を使うのも手ではあるが，そこはぐっと我慢して最後の桁のチェックは別法にて行う。

for (i in c(0, 1, 5, 6)) {
  for (h in c(0, 2, 7)) {
    for (g in c(3, 6)) {
      for (f in c(0, 9)) {
        for (e in c(0, 9)) {
          for (d in c(1, 8)) {
            for (c in c(2, 7)) {
              for (b in c(1, 8)) {
                for (a in 0:9) {
#                  x = ((((((((a*10+b)*10+c)*10+d)*10+e)*10+f)*10+g)*10+h)*10+i)^2
#                  s = as.integer(rev(unlist(strsplit(as.character(x), ""))))
                  s = integer(10)
                  s[1] = i*i
                  s[2] = 2*h*i
                  s[3] = 2*g*i+h*h
                  s[4] = 2*(f*i+g*h)
                  s[5] = 2*(e*i+f*h)+g*g
                  s[6] = 2*(d*i+e*h+f*g)
                  s[7] = 2*(c*i+d*h+e*g)+f*f
                  s[8] = 2*(b*i+c*h+d*g+e*f)
                  s[9] = 2*(a*i+b*h+c*g+d*f)+e*e
                  for (k in 1:9) {
                    if (s[k] > 9) {
                      s[k+1] = s[k+1] + s[k] %/% 10
                      s[k] = s[k] %% 10
                    }
                  }
                  if (length(s) >= 9 && s[1] == i && s[2] == h && s[3] == g && s[4] == f && s[5] == e && s[6] == d && s[7] == c && s[8] == b && s[9] == a) {
                    answer = paste(a, b, c, d, e, f, g, h, i, sep="")
                    print(answer, initLine=FALSE)
                    print(as.bigz(answer)^2)
                  }
                }
              }
            }
          }
        }
      }
    }
  }
}

データの平均値（合計）を求めるとき...

データの性質を見極めておかないと誤った統計数値を得てしまうよという教訓を垂れる訳だろうが...

図に示すような 3 種類のデータがある。各データは 2 列で，1 列目と 2 列目の合計が等しいかどうか判断せよと。

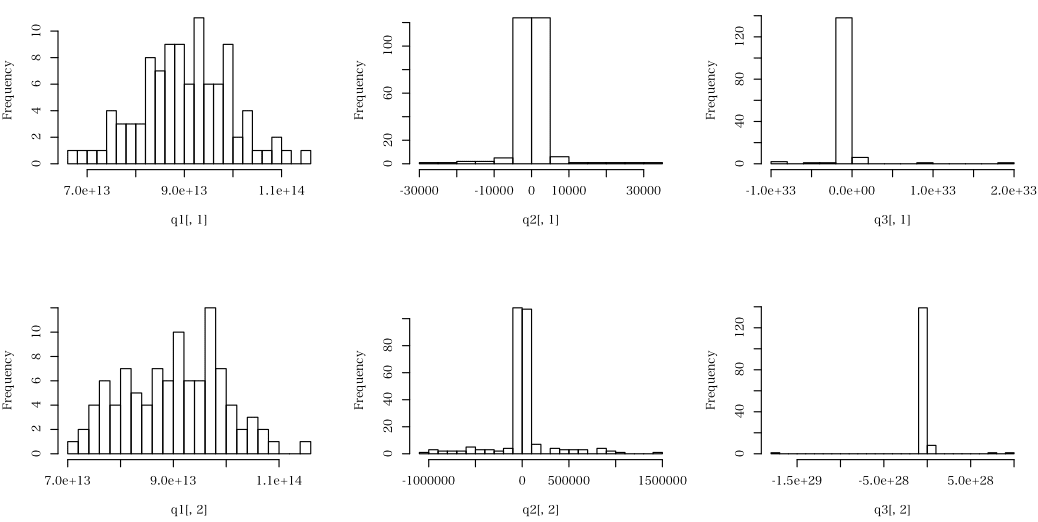
1 番目のデータ（左上が 1 列目，左下が 2 列目）のヒストグラム
　かなり大きな正の値のデータのみ

2 番目のデータ（中上が 1 列目，中下が 2 列目）のヒストグラム
　正・負のデータからなり，絶対値がほどほど大きいデータを少し含む

3 番目のデータ（右上が 1 列目，右下が 2 列目）のヒストグラム
　正・負のデータからなり，外れ値ともいえるような絶対値がめちゃ大きいデータをほんのわずか含む

無邪気に，mean を使ったりすると，

> cat(sum(q1[,1]), sum(q1[,2]))
9007199254740992 9007199254740992

> cat(sum(q2[,1]), sum(q2[,2]))
0 -4.54747350886464e-13

> cat(sum(q3[,1]), sum(q3[,2]))
-71606554540133104 8756878575033.26

のようになる。1 番目のデータの各列の和は等しく，2 番目のデータでは誤差範囲で同じ，3 番目のデータではすごく違いがあるように見えるかもしれないが元のデータのオーダーが 30 桁ほどなんだから，誤差範囲であろうと判断しなければならない。

そもそも，2 番目とか 3 番目のようなデータは実際にはない（オーダーが大きいのは，単位をかえればよいし，普通そのように表されるだろう）ので，そんなに神経質にならなくてもよいのだけど。

それでも，次の様なアルゴリズムで和を求めるというのは，予防的措置として推奨されるかもしれない。

a. 足し算と引き算を混ぜない。正のデータと負のデータを別々に和を求めて，最後に 2 つの和を合計する。

b. 小さな数と大きな数の足し算をしない。小さなものから順に足していく（より慎重にするなら，2 つのデータの和を求めたら，残りのデータと一緒にしてその中の小さな 2 つのデータの和を求めるということを繰り返す）。

以下のようなプログラムを書いてみる。

sum2 = function(d) {
    sum1 = function(x) {
        x1 = x[x > 0]
        x2 = x[x < 0]
        cat(sum(x1), sum(abs(x2)), sum(x1)-sum(abs(x2)), "\n")
        ifelse(length(x1) > 0, tail(cumsum(sort(x1)), 1), 0) -
        ifelse(length(x2) > 0, tail(cumsum(sort(abs(x2))), 1), 0)
    }
    sum1(d[,1]) == sum1(d[,2])
}

これによる結果は，以下のようになる。

> sum2(q1)
9007199254740992 0 9007199254740992
9007199254740992 0 9007199254740992
[1] TRUE

> sum2(q2)
196452.384765625 196452.384765625 0
16530519.4 16530519.4 0
[1] TRUE

> sum2(q3)
2.76019691920891e+33 2.76019691920891e+33 0
1.82694806300339e+29 1.82694806300339e+29 35184372088832
[1] FALSE

3 番目のデータにおいてはまだ誤差範囲であるが同じではないという結果である。

えい，まだるっこしい。

いっそのこと，長精度実数計算をしてしまえ（ただし，上に書いた a, b は考慮する）。

library(Rmpfr)
sum9 = function(d) {
    sum8 = function(x) {
        prec = 200
        x1 = mpfr(x[x > 0], prec)
        x2 = mpfr(x[x < 0], prec)
        s1 = if (length(x1) > 0) tail(cumsum(sort(x1)), 1) else 0
        s2 = if (length(x2) > 0) tail(cumsum(sort(abs(x2))), 1) else 0
        print(c(s1, s2, s1-s2))
        s1-s2
    }
    sum8(d[,1]) == sum8(d[,2])
}

これによれば，全てのデータセットで，2 列の合計値は等しくないということがはっきりする。

そして，その差は誤差範囲であるということである。

> sum9(q1)
3 'mpfr' numbers of precision  128 .. 200  bits
[1] 9007199254740993                0 9007199254740993
3 'mpfr' numbers of precision  128 .. 200  bits
[1] 9007199254740992                0 9007199254740992
[1] FALSE

> sum9(q2)
3 'mpfr' numbers of precision  200   bits
[1] 196452.384765625 196452.384765625                0
3 'mpfr' numbers of precision  200   bits
[1]         16530519.40000000000000479616346638067625463008880615234375
[2]        16530519.399999999999994582111639829236082732677459716796875
[3] 1.0214051826551440171897411346435546875000000000000000000000000e-14
[1] FALSE

> sum9(q3)
3 'mpfr' numbers of precision  200   bits
[1]  2760196919208909839959496867497081.8282129668101326662451169565
[2]  2760196919208909911700429409141880.8282129668101326104341159326
[3] -71740932541644798.999999999999999944188998976167179947377656232
3 'mpfr' numbers of precision  200   bits
[1] 182694806300338729143596181240.44380035052800129831732213181835
[2] 182694806300338720381823051512.44380035052800286368844502856631
[3] 8761773129727.9999999999999984346288771032520431883572850254938
[1] FALSE