一夜干しの効果

今流行の ChatGPT に聞いてみました

----- 質問

一夜干しすると栄養価が増すなんていうけで，水分が抜けるために，重量比で言えばそうなるというだけじゃないのか？

----- お返事

一夜干しによって栄養価が増すという主張は、完全に正確ではありません。一夜干しによって、食材の重量は減少するため、重量比で栄養価が増すと見えるかもしれませんが、それは栄養価が実際に増加していることを意味しません。

ただし、一夜干しによって、食材の保存期間が延びることがあります。また、一夜干しによって、食材中の水分量が減少するため、重量比で栄養素の濃度が高くなる場合があります。たとえば、乾燥したフルーツは、同じ量の生のフルーツよりも糖分が濃縮されているため、より甘く感じることがあります。

しかし、一夜干しによって栄養素の損失も発生する可能性があるため、必ずしも栄養価が増すわけではありません。また、一夜干しによって微生物の増殖が防止されるため、食中毒のリスクが低くなることがあるため、食材の安全性も向上することがあります。

総合的に考えると、一夜干しによって栄養価が増すという主張は、一般的には正確ではありません。ただし、食材の保存期間や風味、食中毒のリスクなどに影響を与える可能性があるため、適切に行われる場合にはメリットがあることもあります。
----- 終わり

 

怪しい広告

糖質低減炊飯器

>「糖質を低減できる」として人気の炊飯器について、国民生活センターは4つのメーカーの製品で「広告表示ほどの効果が無かった」と発表しました。

だよね。なんで，こんなバカバカしい謳い文句に騙されるんだろう。大原則「質量保存の法則」を知らないんだろうね。販売者側も知らなかったとは思えず，消費者を騙そうという魂胆がミエミエ。

職人の技も，数学を応用すべし。

今，テレビでやってた。クロワッサンを作るときに，最適なバターの割合をx%からはじめてx+1%にしてとやって，20年かかってやっと最適な割合を見つけたんですって。

ご苦労様でした。二分法を知っていれば，もっと速く最適な割合が見つかったんでしょうにねえ。

数学は偉大だよ。

算額（その168）

算額（その168）

岐阜県大垣市西外側町 大垣八幡神社 天保年間
http://ryugen3.sakura.ne.jp/toukou3/wasankibousya.PDF

第20問: 正三角形内に等しい 3 円弧を描き，その中に青円，萌黄円を 3 個ずつ入れる。青円の直径を知って萌黄円の直径を求めよ。

正三角形の頂点を通る円の半径を 1 とし，萌黄円，青円の半径を r1，r2とおく。r1 は簡単に求めることができる。r2 を求め，r1/r2 の比を求める。

using SymPy

@syms r2::positive;
sine = sin(PI/6)
cosine = cos(PI/6)
r0 = 1
xy = r0*sine - r2
x2 = xy*cosine
y2 = xy*sine
eq1 = x2^2 + (y2 + r0)^2 - (1 + r2)^2 |> simplify
eq1 |> println

   3/4 - 4*r2

res = solve(eq1)[1] |> println  # r2

   3/16

x2 |> simplify |> println
y2 |> simplify |> println

   sqrt(3)*(1 - 2*r2)/4
   1/4 - r2/2

r1 = r0 - r0*cosine
r2 = 3//16
r1/r2 |> simplify |> println

   16/3 - 8*sqrt(3)/3

萌黄径 = (16/3 - 8*sqrt(3)/3) × 青径 = 0.714531179816327 × 青径 である。

using Plots

function circle(ox, oy, r, color=:red; beginangle=0, endangle=360, fill=false)
   θ = beginangle:0.1:endangle
   x = r.*cosd.(θ)
   y = r.*sind.(θ)
   if fill
       plot!(ox .+ x, oy .+ y, linecolor=color, linewidth=0.5, seriestype=:shape, fillcolor=color)
   else
       plot!(ox .+ x, oy .+ y, color=color, linewidth=0.5)
   end
end;

function point(x, y, string="", color=:green, position=:left, vertical=:top; mark=true)
   mark && scatter!([x], [y], color=color, markerstrokewidth=0)
   annotate!(x, y, text(string, 10, position, color, vertical))
end;

function draw(R, more)
    pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   sine   = sin(PI/6)
   cosine = cos(PI/6)
   r0 = 1
   r1 = r0 - r0*cosine
   r2 = 3//16
   (x2, y2) = (sqrt(Sym(3))*(1 - 2*r2)/4, 1//4 - r2/2)
   println("萌黄径/青径 = $(r1/r2) = $((r1/r2).evalf())")
   plot()
   circle(0, r0/2, r1, :olivedrab1, fill=true)
   circle(r0/2*cosine, -r0/2*sine, r1, :olivedrab1, fill=true)
   circle(-r0/2*cosine, -r0/2*sine, r1, :olivedrab1, fill=true)
   circle(x2, y2, r2, :steelblue1, fill=true)
   circle(-x2, y2, r2, :steelblue1, fill=true)
   circle(0, -sqrt(x2^2 + y2^2), r2, :steelblue1, fill=true)
   circle(r0*cosine, r0*sine, r0, beginangle=150, endangle=270)
   circle(-r0*cosine, r0*sine, r0, beginangle=270, endangle=390)
   circle(0, -r0, r0, beginangle=30, endangle=150)
   plot!([r0*cosine, 0, -r0*cosine, r0*cosine], [-r0*sine, r0, -r0*sine, -r0*sine], color=:black, lw=0.5)
   if more == true
       point(x2, y2, "(x2,y2,r2)", :black, :top)
       point(0, r0/2, " r0/2", :black)
       point(r0*cosine, r0*sine, "", :red)
       point(-r0*cosine, r0*sine, "", :red)
       point(0, -r0, "", :red)
       circle(0, 0, 1, :black)
       hline!([0], color=:black, lw=0.5)
       vline!([0], color=:black, lw=0.5)
   else
       plot!(showaxis=false)
   end
end;

draw(123, true)

   萌黄径/青径 = 16/3 - 8*sqrt(3)/3 = 0.714531179816327

 

算額（その167）

算額（その167）

岐阜県大垣市西外側町 大垣八幡神社 天保年間
http://ryugen3.sakura.ne.jp/toukou3/wasankibousya.PDF

第17問: 外接する 2 個の円と共通接線の間に青と黒の正方形を置く，黃円の径を知って黒の正方形の一辺の長さを求めよ。

図のように青と黒の正方形の右下隅の x 座標を x1, x2，円の半径を r として，連立方程式を解く。

using SymPy

@syms r::positive, x1::positive, x2::positive;

eq1 = (r - x1)^2 + (r - 2x1)^2 - r^2
eq2 = (r - x2)^2 + (r - x2 + x1)^2 - r^2
res = solve([eq1, eq2], (x1, x2))

   4-element Vector{Tuple{Sym, Sym}}:
    (r/5, 2*r/5)
    (r/5, 9*r/5)
    (r, r)
    (r, 2*r)

題意を満たすのは (r/5, 2*r/5) である。r は半径なので，黒の正方形の一辺の長さは黃円の直径の 1/10 である。

using Plots

function circle(ox, oy, r, color=:red; beginangle=0, endangle=360, fill=false)
   θ = beginangle:0.1:endangle
   x = r.*cosd.(θ)
   y = r.*sind.(θ)
   if fill
       plot!(ox .+ x, oy .+ y, linecolor=color, linewidth=0.5, seriestype=:shape, fillcolor=color)
   else
       plot!(ox .+ x, oy .+ y, color=color, linewidth=0.5)
   end
end;

function point(x, y, string="", color=:green, position=:left, vertical=:top; mark=true)
   mark && scatter!([x], [y], color=color, markerstrokewidth=0)
   annotate!(x, y, text(string, 10, position, color, vertical))
end;

function rect(x1, y1, x2, y2, color=:pink)
   plot!([x1, x2, x2, x1, x1], [y1, y1, y2,  y2, y1], color=color, linewidth=0.5, seriestype=:shape, fillcolor=color)
end;

function draw(R, more)
    pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   r = R / 2
   (x1, x2) = (r/5, 2*r/5)
   plot()
   println("黃径 = $R, 黒一辺 = $(x2 - x1), 青一辺 $(2x1)")
   circle(r, r, r, :yellow, fill=true)
   circle(-r, r, r, :yellow, fill=true)
   rect(-x1, 0, x1, 2x1, :blue)
   rect(x1, 0, x2, x2 - x1, :black)
   rect(-x1, 0, -x2, x2 - x1, :black)
   if more == true
       point(r, r, "(r,r,r)", :black)
       point(x1, 0, "x1", :black, :top)
       point(x2, 0, "x2", :black, :top)
       hline!([0], color=:black, lw=0.5)
       vline!([0], color=:black, lw=0.5)
   else
       plot!(showaxis=false)
   end
end;

draw(123, true)

   黃径 = 123, 黒一辺 = 12.3, 青一辺 24.6

算額（その166）

算額（その166）

岐阜県大垣市西外側町 大垣八幡神社 天保年間
http://ryugen3.sakura.ne.jp/toukou3/wasankibousya.PDF

第17問: 長方形内に半円（萌黄）と円弧を描き，その中に赤円と黒円を入れる。赤円と黒円の直径を知って長方形の長い方の一辺の長さを求めよ。

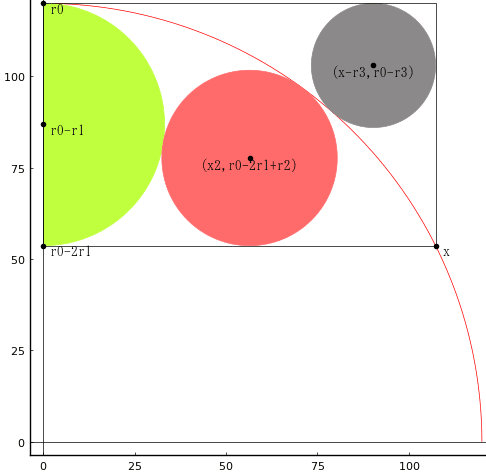
図のように記号を定め，連立方程式を解く。

using SymPy

@syms 　r0::positive, r1::positive, r2::positive, r3::positive, x2::positive, x::positive;

r2 = 24
r3 = 17
eq1 = x2^2 + (r0 - 2r1 + r2)^2 - (r0 - r2)^2
eq2 = (x - r3)^2 + (r0 - r3)^2 - (r0 + r3)^2
eq3 = x2^2 + (r1 - r2)^2 - (r1 + r2)^2
eq4 = (r0 - 2r1)^2 + x^2 - r0^2;

res = solve([eq1, eq2, eq3, eq4], (r0, r1, x2, x))

   2-element Vector{NTuple{4, Sym}}:
    (289*sqrt(102)/49 + 11849/196, -17*sqrt(186001 + 19528*sqrt(102))/392 + 289*sqrt(102)/98 + 11849/392, sqrt(-204*sqrt(186001 + 19528*sqrt(102))/49 + 13872*sqrt(102)/49 + 142188/49), 34*sqrt(102)/7 + 408/7)
    (289*sqrt(102)/49 + 11849/196, 17*sqrt(186001 + 19528*sqrt(102))/392 + 289*sqrt(102)/98 + 11849/392, sqrt(204*sqrt(186001 + 19528*sqrt(102))/49 + 13872*sqrt(102)/49 + 142188/49), 34*sqrt(102)/7 + 408/7)

赤円，黒円の径が 24, 17 のとき，長方形の長い方の一辺の長さは (408 + 34√102)/7 = 107.34045255775867 である。
術文では，「黒径 / (1 - sqrt(黒径 / 赤径))」 であるが，SymPy では 「(sqrt(赤径)*黒径^1.5 + 赤径*黒径)/(赤径 - 黒径)」までしか簡単にならない。

(408 + 34√102)/7, (sqrt(r2)*r3^1.5 + r2*r3)/(r2 - r3), r3 / (1 - sqrt(r3 / r2))

   (107.34045255775867, 107.34045255775865, 107.34045255775871)

using Plots

function circle(ox, oy, r, color=:red; beginangle=0, endangle=360, fill=false)
   θ = beginangle:0.1:endangle
   x = r.*cosd.(θ)
   y = r.*sind.(θ)
   if fill
       plot!(ox .+ x, oy .+ y, linecolor=color, linewidth=0.5, seriestype=:shape, fillcolor=color)
   else
       plot!(ox .+ x, oy .+ y, color=color, linewidth=0.5)
   end
end;

function point(x, y, string="", color=:green, position=:left, vertical=:top; mark=true)
   mark && scatter!([x], [y], color=color, markerstrokewidth=0)
   annotate!(x, y, text(string, 10, position, color, vertical))
end;

function draw(more)
    pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (r2, r3) = (24, 17)
   (r0, r1, x2, x) = res[1]
   r0 < 2r1 && ((r0, r1, x2, x) = res[2])
   println("r0 = $r0;  r1 = $r1;  x2 = $x2\nx = $x = $(x.evalf())")
   plot()
   circle(0, 0, r0, beginangle=0, endangle=90)
   circle(0, r0 - r1, r1, :olivedrab1, beginangle=270, endangle=450, fill=true)
   circle(x2, r0 - 2r1 + r2, r2, :indianred1, fill=true)
   circle(x - r3, r0 - r3, r3, :snow4, fill=true)
   plot!([0, x, x, 0, 0], [r0 - 2r1, r0 - 2r1, r0, r0, r0 - 2r1], color=:black, lw=0.5)
   if more == true
       point(0, r0, " r0", :black, :left)
       point(0, r0 - r1, " r0-r1", :black, :left)
       point(0, r0 - 2r1, " r0-2r1", :black, :left)
       point(x2, r0 - 2r1 + r2, "(x2,r0-2r1+r2)", :black, :top)
       point(x - r3, r0 - r3, "(x-r3,r0-r3)", :black, :top)
       point(x, r0 - 2r1, " x", :black)
       hline!([0], color=:black, lw=0.5)
       vline!([0], color=:black, lw=0.5)
   else
       plot!(showaxis=false)
       plot!(xlims=(0,112), ylims=(50, 125))
   end
end;

draw(false)

   r0 = 289*sqrt(102)/49 + 11849/196;  r1 = -17*sqrt(186001 + 19528*sqrt(102))/392 + 289*sqrt(102)/98 + 11849/392;  x2 = sqrt(-204*sqrt(186001 + 19528*sqrt(102))/49 + 13872*sqrt(102)/49 + 142188/49)
   x = 34*sqrt(102)/7 + 408/7 = 107.340452557759