算額(その1621)
京都市東山区 安井金比羅宮
近畿数学史学会:近畿の算額「数学の絵馬を訪ねて」,平成4年5月16日 初版第一刷,大阪教育図書株式会社,大阪市.
・ 奉納算題四季詠の五月問題
平成元年(1989)正月 奉納絵馬
http://www.wasan.jp/kyoto/yasuikonpira2.html
大橋彪正:和算を用いた数学教育
https://www.st.nanzan-u.ac.jp/info/gr-thesis/2019/koto/pdf/16ss056.pdf
キーワード:九曜紋
#Julia, #SymPy, #算額, #和算, #数学
幟をそむる事有定紋の図を見るに九曜也惣径二尺あるときは大小の円径各いかにと問
注:惣径 = 大円径 + 2*小円径 である。
惣径を K
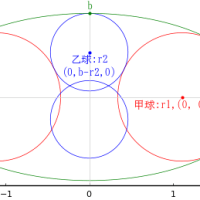
大円の半径と中心座標を R, (0, 0)
小円の半径と中心座標を r, (0, R + r)
とおき,以下の連立方程式を解く。
include("julia-source.txt");
# julia-source.txt ソース https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf
using SymPy
@syms n::integer, R::positive, r::positive, K::positive
n = 9
R = K/2 - 2r
eq = (R + r)*sind(Sym(180)/(n - 1)) - r
res = solve(eq, r)[1];
# r 小円径
res |> println
res
K*sqrt(2 - sqrt(2))/(2*sqrt(2 - sqrt(2)) + 4)

sqrt(2 - sqrt(2)) が 2 回出てくるので,これを t とおくと K*t/(2*(t + 2)) のように簡単になる。
なお,sin(π/8) = sqrt(2 - sqrt(2))/2 = 0.3826834323650898 である。
@syms t
res(sqrt(2 - √Sym(2)) => t) |> factor |> println
K*t/(2*(t + 2))
半径を直径にして,術風に書くと算額の術より短くなる。
惣径 = 20
人 = sqrt(2 - √2)
小円径 = 惣径*人/(人 + 2)
大円径 = 惣径 - 2*小円径
(小円径, 大円径)
(5.535373078283104, 8.929253843433791)
算額の術は以下のようになっている。
惣径 = 20
天 = (√2 + 1)^2
小円径 = ((√(天 + 1) - 1) / 天)*惣径
大円径 = 惣径 - 2*小円径
(小円径, 大円径)
(5.535373078283104, 8.929253843433791)
function draw(K, more=false)
pyplot(size=(1000, 1000), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
t = sqrt(2 - sqrt(2))
r = K/2*t/(t + 2)
R = K/2 - 2r
@printf("惣径が %d のとき,大円径 = %g,小円径 = %g である。\n", K, 2R, 2r)
plot()
circlef(0, 0, R, :orange)
rotatef(0, r + R, r, :pink, angle=360/8)
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
hline!([0], color=:gray80, lw=0.5)
vline!([0], color=:gray80, lw=0.5)
end
end;
draw(20, true)