算額（その1464）

算額（その1464）

百二十 清水寺 群馬県高崎市石原町 明治6年(1873)
群馬県和算研究会:群馬の算額，上武印刷株式会社，高崎市，1987年3月31日.
キーワード：円弧，弓形，面積
#Julia, #SymPy, #算額, #和算

円弧（弓形）の面積と弦の長さが与えられたとき，円の直径はいかほどか。

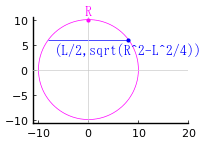
円の半径を R，円弧の面積を S，弦の長さを L とおき，以下の方程式を解く。

solve は対応できないので，find_zero で数値解を求める。

include("julia-source.txt");
# julia-source.txt ソース　https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cfusing SymPy

using SymPy
@syms R::positive, S::positive, L::positive, θ::positive, K::positive
L = 16
S = 44.7295218001612
θ = asind((L/2)/R)
eq = S - (2θ/360*PI*R^2 - (L/2)*sqrt(R^2 - (L/2)^2));

# solve(eq, R)
using Roots
find_zero(eq, (L/2, L))

    10.000000000000004

積分により，検算する。

R = 10
integrate(sqrt(R^2 - x^2) - 6, (x, -8, 8)).evalf() |> println

    44.7295218001612

function draw(R, L, more)
    pyplot(size=(200, 200), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
    plot()
    circle(0, 0, R, :magenta)
    x = L/2
    y = sqrt(R^2 - x^2)
    segment(-x, y, x, y, :blue)
    if more
        delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
        hline!([0], color=:gray80, lw=0.5)
        vline!([0], color=:gray80, lw=0.5)
        point(0, R, "R", :magenta, :center, :bottom, delta=delta)
        point(L/2, sqrt(R^2 - L^2/4), "(L/2,sqrt(R^2-L^2/4))", :blue, :center, delta=-3delta)
        xlims!(-11, 20)
    end
end;

draw(20/2, 16, true)