算額（その1463）

算額（その1463）

七十五 群馬県吾妻町三島 馬頭観世音 嘉永4年(1851)
群馬県和算研究会:群馬の算額，上武印刷株式会社，高崎市，1987年3月31日.
キーワード：円6個，直角三角形，正五角形
#Julia, #SymPy, #算額, #和算

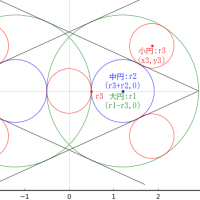
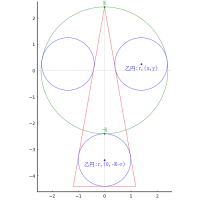
直角三角形の中に正五角形，大円 5 個，小円 1 個を容れる。大円は正五角形に内接し，大円，小円は互いに外接し合っている。股，弦がそれぞれ 15 寸，17 寸のとき，大円の直径はいかほどか。

注：「股，弦がそれぞれ 15 寸，17 寸のとき」正五角形は図のようには内接しない。

正五角形の外接円の半径と中心座標を R, (0, 0)
大円の半径と中心座標を r1, (0, r2 + r1)
小円の半径と中心座標を r2, (0, 0)
とおく。

小円の半径 r2 が既知として，以下の連立方程式を解き R, r1 を求める。 また，外接円の半径がわかれば，正五角形が内接する直角三角形の頂点座標および鈎，股，弦の長さは簡単に計算できる。
R, r2, 鈎, 股, 弦が特定の値を取るときの r1 は比例計算で求められる。

include("julia-source.txt");
# julia-source.txt ソース　https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cfusing SymPy

using SymPy
@syms R::positive, r1::positive, x1::positive, y1::positive,
      r2::positive
eq1 = r1 - (r1 + r2)*sind(Sym(36))
eq2 =  r1 - (R - r1 - r2)*cosd(Sym(36));
res = solve([eq1, eq2], (R, r1));

# R
@syms t  # = sqrt(5-sqrt(Sym(5)))
res[R](sqrt(5-sqrt(Sym(5))) => t) |> simplify |> println

    2*r2*(2*t + sqrt(2) + sqrt(10))/(-sqrt(5)*t - t + 2*sqrt(2) + 2*sqrt(10))

# r1
res[r1](sqrt(5-sqrt(Sym(5))) => t) |> simplify |> println

    -r2*t/(t - 2*sqrt(2))

小円の半径 r2 が 1/2 のとき
大円径 = 1.42592;  外円径 = 4.18845;  鈎 = 5.23557; 股 = 7.20614;  弦 = 8.90728

「答曰大円径二寸六分二厘有奇」なので，大円径が 2.62 寸のときは小円の半径は 1.83741023576469/2 で，そのとき
大円径 = 2.62;  外円径 = 7.69591;  鈎 = 9.61989; 股 = 13.2406;  弦 = 16.3663

股は 15 寸ではなく，弦も 17 寸ではない。

function draw(r2, more)
    pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
    t = sqrt(5 - √5)
    u = √2 + √10
    R = 2r2*(2t + u)/(2u - √5t - t)
    r1 = r2*t/(2√2 - t)
    θ = range(start=90, step=72, length=6)
    x = R.*cosd.(θ)
    y = R.*sind.(θ)
    (x1, y1) = float.(intersection(x[1], y[1], x[2], y[2], x[3], y[3], x[4], y[4]))
    (x2, y2) = float.(intersection(x[1], y[1], x[2], y[2], x[5], y[4], x[5], y[5]))
    (鈎, 股) = (y2 - y1, x2 - x1)
    弦 = sqrt(鈎^2 + 股^2)
    @printf("大円径 = %g;  外円径 = %g;  鈎 = %g; 股 = %g;  弦 = %g\n", 2r1, 2R, 鈎, 股, 弦)
    circle(0, 0, R)
    plot(x, y, color=:green, lw=0.5, axis=false)
    circle(0, 0, r2, :magenta)
    rotate(0, r1 + r2, r1, :blue, angle=72)
    #segment(x[5], y[4], x1, y1)
    #segment(x[5], y[4], x2, y2)
    #segment(x1, y1, x2, y2)
    plot!([x1, x2, x2, x1], [y1, y1, y2, y1], color=:red, lw=0.5)
    if more
        delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
        hline!([0], color=:gray80, lw=0.5)
        vline!([0], color=:gray80, lw=0.5)
        point(x1, y1, "(x1,y1)", :red, :left, delta=-delta)
        point(x2, y2, " (x2,y2)", :red, :right, :bottom, delta=delta)
        point(x2, y1, " (x2,y1)", :red, :right, delta=-delta)
        point(0, r2 + r1, "大円:r1\n(0,r2+r1)", :blue, :center, delta=-delta)
        point(0, 0, "小円:r2", :magenta, :center, delta=-delta)
    end
end;

draw(1.83741023576469/2, true)