本場 讃岐うどん たも屋 三条店

高松市三条町 本場 讃岐うどん たも屋 三条店
朝8時開店は早い方です

算額（その1466）

算額（その1466）

百二十六 群馬県倉渕村水沼 蓮華院 明治11年(1878)
群馬県和算研究会:群馬の算額，上武印刷株式会社，高崎市，1987年3月31日.
キーワード：円，三分割
#Julia, #SymPy, #算額, #和算

円を面積が等しくなるように 2 本の平行な弦（等線）を引き，3 等分する。円の直径が与えられたとき，等線の長さはいかほどか。」

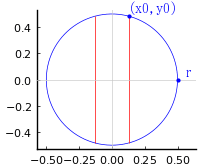
本問の胆は「円を平行な直線 2 本で三分割する方法」である。
このブログでも算額とは無関係にすでに 2 回取り上げている。
「ホールケーキを三等分する」，「1/3 ずつに分割せよ...変わったケーキカット」

それぞれ，アプローチの仕方は異なるが，今回は簡明直截に SymPy の integrate を使い，等線の長さを求める。
円の半径を 1/2 とする。sqrt(r^2 - x^2) を x0 < x < r まで積分する。

include("julia-source.txt");
# julia-source.txt ソース　https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf

using SymPy
using Roots
@syms r::positive, x::positive, x0::positive
r = 1/2
eq = 2integrate(sqrt(r^2 - x^2), (x, x0, r)) - PI*r^2/3
ans_x0 = find_zero(eq, (0, r))

    0.13246604230138845

直径 1 の円を 3 分割する等線の長さは 2y0 = 2sqrt(r^2 - ans_x0^2) = 0.9642670742838972

2sqrt(r^2 - ans_x0^2)

    0.9642670742838972

「術」によれば，円の直径*(1/1.036933) = 0.9643824625120426

function draw(more)
    pyplot(size=(200, 200), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
    r = 1/2
    x0 = 0.13246604230138845
    y0 = sqrt(r^2 - x0^2)
    println("x0 = $x0, y0 = $y0, 2y0 = $(2y0)")
    plot()
    circle(0, 0, r, :blue)
    segment(x0, y0, x0, -y0, :red)
    segment(-x0, y0, -x0, -y0, :red)
    if more
        delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
        hline!([0], color=:gray80, lw=0.5)
        vline!([0], color=:gray80, lw=0.5)
        point(x0, y0, "(x0,y0)", :blue, :left, :bottom, delta=delta/2)
        point(r, 0, " r", :blue, :left, :bottom, delta=delta/2)
        xlims!(-r - 5delta, r + 10delta)
    end
end;

draw(true)

算額（その1465）

算額（その1465）

百二十一 群馬県藤岡市藤岡 龍源寺 明治6年(1873)
群馬県和算研究会:群馬の算額，上武印刷株式会社，高崎市，1987年3月31日.
キーワード：球4個，半球，3次元
#Julia, #SymPy, #算額, #和算

「文面は判読できない」とあるが，「半球の中に，半球に内接し，互いに外接し合う 4 個の等球を容れる。半球の直径が与えられたとき，等球の直径はいかほどか。」でもあろう。

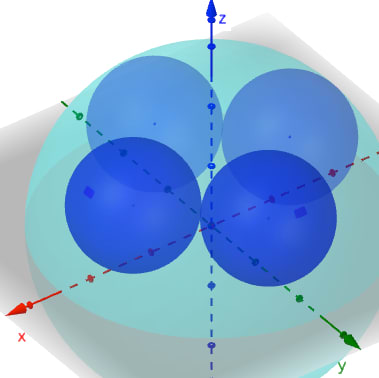
左の図は上から x-y 平面を見た様子，右の図は x 軸の正の位置から y-z 平面を見た様子。

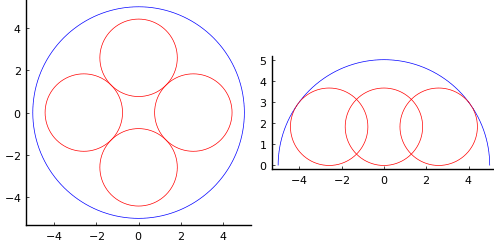
半球の半径と中心座標を r1, (0, 0, 0)
等球の半径と中心座標を r2, (x2, 0, r2), (0, x2, r2)
とおき，以下の連立方程式を解く。

include("julia-source.txt");
# julia-source.txt ソース　https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813

using SymPy
@syms r1::positive, r2::positive, x2::positive
eq1 = x2^2 + r2^2 - (r1 - r2)^2
eq2 = 2x2^2 - 4r2^2
res = solve([eq1, eq2], (r2, x2))[1];  # 1 of 2

# r2
res[1] |> simplify |> println

    r1*(-1 + sqrt(3))/2

# x2
res[2] |> sympy.sqrtdenest |> println

    r1*(-sqrt(2)/2 + sqrt(6)/2)

等球の半径は半球の半径の (√3 - 1)/2 倍である。
半球の直径が 10 寸のとき，等球の直径は 3.660254037844386 寸である。

function draw(r1, more)
    pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
    r2= r1*(√3 - 1)/2
    x2 = r1*(√6 - √2)/2
    @printf("r1 = %.15g;  r2 = %.15g;  x2 = %.15g\n", r1, r2, x2)
    p1 = plot()
    circle(0, 0, r1, :blue)
    circle42(0, x2, r2)
    if more
        delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
        hline!([0], color=:gray80, lw=0.5)
        vline!([0], color=:gray80, lw=0.5)
    end
    p2 = plot()
    circle(0, 0, r1, :blue, beginangle=0, endangle=180)
    circle2(x2, r2, r2)
    circle(0, r2, r2)
    plot(p1, p2)
end;

draw(10/2, false)

算額（その1464）

算額（その1464）

百二十 清水寺 群馬県高崎市石原町 明治6年(1873)
群馬県和算研究会:群馬の算額，上武印刷株式会社，高崎市，1987年3月31日.
キーワード：円弧，弓形，面積
#Julia, #SymPy, #算額, #和算

円弧（弓形）の面積と弦の長さが与えられたとき，円の直径はいかほどか。

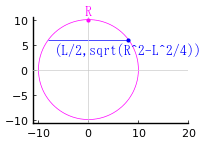
円の半径を R，円弧の面積を S，弦の長さを L とおき，以下の方程式を解く。

solve は対応できないので，find_zero で数値解を求める。

include("julia-source.txt");
# julia-source.txt ソース　https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf

using SymPy
@syms R::positive, S::positive, L::positive, θ::positive, K::positive
L = 16
S = 44.7295218001612
θ = asind((L/2)/R)
eq = S - (2θ/360*PI*R^2 - (L/2)*sqrt(R^2 - (L/2)^2));

# solve(eq, R)
using Roots
find_zero(eq, (L/2, L))

    10.000000000000004

積分により，検算する。

R = 10
integrate(sqrt(R^2 - x^2) - 6, (x, -8, 8)).evalf() |> println

    44.7295218001612

function draw(R, L, more)
    pyplot(size=(200, 200), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
    plot()
    circle(0, 0, R, :magenta)
    x = L/2
    y = sqrt(R^2 - x^2)
    segment(-x, y, x, y, :blue)
    if more
        delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
        hline!([0], color=:gray80, lw=0.5)
        vline!([0], color=:gray80, lw=0.5)
        point(0, R, "R", :magenta, :center, :bottom, delta=delta)
        point(L/2, sqrt(R^2 - L^2/4), "(L/2,sqrt(R^2-L^2/4))", :blue, :center, delta=-3delta)
        xlims!(-11, 20)
    end
end;

draw(20/2, 16, true)