算額(その1607)
宮城県石巻市尾崎宮下 久須師神社 明治20年(1887)
徳竹亜紀子,谷垣美保:2021年度の算額調査,仙台高等専門学校名取キャンパス研究紀要,第 58 号(2022),p.7-28.
https://www.sendai-nct.ac.jp/natori-library/wp-content/uploads/2022/03/kiyo2022-2.pdf
キーワード:円2個,円弧2個,斜線
#Julia, #SymPy, #算額, #和算, #数学
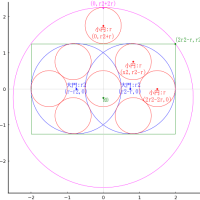
交差する円弧の中に等円を 2 個と共通接線を入れる。短径,長径,等円の直径が与えられたとき,共通接線と円弧の交点間の距離(斜の長さ)を求める術を述べよ。

等円の半径を r
円弧を構成する円の半径と中心座標を R, (0, 0)
等円の半径と中心座標を r, (x, y)
共通接線と円弧の交点座標を (x0, y0)
短径を 2K1, 長径を 2K2
とおく。
AB= K1 = R - y
BC = K2 = sqrt(R^2 - y^2) である。
以下の連立方程式を解き,(x0, y0, y, x, R) を求める。
これらは,K1, K2 を含む式で表される。
include("julia-source.txt");
# julia-source.txt ソース https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf
using SymPy
@syms R::positive, x::positive,
y::positive, r::positive,
x0::positive, y0::positive,
K1::positive, K2::positive
eq1 = x^2 + y^2 - (R - r)^2
eq2 = r/x - (y0 - y)/sqrt(x0^2 + (y0 - y)^2)
eq3 = x0^2 + y0^2 - R^2
eq4 = (R - y) - K1
eq5 = sqrt(R^2 - y^2) - K2
res = solve([eq1, eq2, eq3, eq4, eq5], (x0, y0, y, x, R))[4]
(K2^2*sqrt(-1/(K1*r - K2^2))*sqrt((K1^2*r - K1*K2^2 + K2^2*r)/(K1*r - K2^2))/sqrt(K1), (-K1^3*r + K1^2*K2^2 - K1*K2^2*r - K2^4)/(2*K1*(K1*r - K2^2)), (-K1^2 + K2^2)/(2*K1), sqrt(-(K1 - r)*(K1*r - K2^2))/sqrt(K1), (K1^2 + K2^2)/(2*K1))
斜の長さは 2sqrt(x0^2 + (y0 - y)^2) である。
# x0^2
x2 = res[1]^2 |> simplify
x2 |> println
K2^4*(-K1^2*r + K1*K2^2 - K2^2*r)/(K1*(K1*r - K2^2)^2)
# (y0 - y)^2
y2 = (res[2] - res[3])^2 |> simplify
y2 |> println
K2^4*r^2/(K1^2*r^2 - 2*K1*K2^2*r + K2^4)
# 斜 = 2sqrt(x0^2 + (y0 - y)^2)
斜 = x2 + y2 |> simplify |> x -> sqrt(x) |> simplify |> x -> 2x

斜(K1 => 8/2, K2 => 16/2, r => 5/2) |> println
10.6666666666667
徳竹も方法(経路)は違うが,結果として同じ式を導いている。
# 短径,長径,等円径はそれぞれの 1/2 で指定する
@syms 短径, 長径, 等円径
徳竹 = 長径^2*sqrt((短径 - 等円径)/(短径*(長径^2 - 短径*等円径)))

2*徳竹(短径 => 8/2, 長径 => 16/2, 等円径 => 5/2)|> println
10.6666666666667
function draw(K1, K2, r, more=false)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
(x0, y0, y, x, R) = (K2^2*sqrt(-1/(K1*r - K2^2))*sqrt((K1^2*r - K1*K2^2 + K2^2*r)/(K1*r - K2^2))/sqrt(K1), (-K1^3*r + K1^2*K2^2 - K1*K2^2*r - K2^4)/(2*K1*(K1*r - K2^2)), (-K1^2 + K2^2)/(2*K1), sqrt(-(K1 - r)*(K1*r - K2^2))/sqrt(K1), (K1^2 + K2^2)/(2*K1))
斜 = sqrt(x0^2 + (y0 - y)^2)
@printf("短径 = %g,長径 = %g,等円径 = %g のとき,斜の長さ = %g\n", 2K1, 2K2, 2r, 2斜)
plot()
θ = atand(y/sqrt(R^2 - y^2))
circle(0, 0, R, beginangle=θ, endangle=180-θ, n=1000)
circle(0, 2y, R, beginangle=180+θ, endangle=360-θ, n=1000)
circle(x, y, r, :green)
circle(-x, y, r, :green)
segment(-x0, y - (y0 - y), x0, y0, :blue)
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
hline!([0], color=:gray80, lw=0.5)
vline!([0], color=:gray80, lw=0.5)
point(x, y, "等円:r,(x,y)", :green, :center, delta=-delta)
point(0, R, "R", :red, :center, :bottom, delta=delta)
point(0, y, " y", :blue, :left, :vcenter)
point(x0, y0, "(x0,y0)", :blue, :left, :bottom, delta=delta)
dimension_line(0, y, sqrt(R^2 - y^2), y, "K2", :magenta, :center, :bottom, delta=2delta)
dimension_line(0, R, 0, y, "K1 ", :orange, :right, :vcenter)
end
end;
draw(8/2, 16/2, 5/2, true)png)