算額（その1341）

算額（その1341）

岐阜県垂井町 西法寺 令和6年(2024)
http://www.wasan.jp/gifu/saihoji.html
算法点竄指南録　百三
https://kokusho.nijl.ac.jp/biblio/100301503/49?ln=ja

キーワード：円4個，直線上
#Julia, #SymPy, #算額, #和算

直線上に，甲円，乙円，丙円，丁円を載せる。甲円，乙円の直径が 25 寸，1 寸のとき，乙円，丁円の直径はいかほどか。

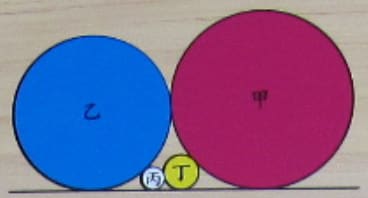
甲円，乙円，丙円，丁円の直径を d1, d2, d3, d4 とおくと，
甲円と乙円の中心の水平距離 = sqrt(d1, d2)
乙円と丙円の中心の水平距離 = sqrt(d2, d3)
丙円と丁円の中心の水平距離 = sqrt(d3, d4)
丁円と甲円の中心の水平距離 = sqrt(d4, d1)
で，以下が成り立つ。
sqrt(d1*d2) = sqrt(d2*d3) + sqrt(d3*d4) + sqrt(d4*d1)
d1 = 25, d3 = 1 なので，
sqrt(25d2) = sqrt(d2) + sqrt(d4) + sqrt(25d4)
5√d2 = √d2 + √d4 + 5√d4
4√d2 = 6√d4
である。
この条件を満たす d2, d4 の整数解は d2 = 9, d4 = 4 である。
乙円の直径は 9 寸，丙円の直径は 4 寸である。

しかし，（答えは合っているのだが）この条件で図を描くと算額の図とは異なるものになる。
丁円と乙円が交わってしまう。

include("julia-source.txt");

function draw(d1, d3, more)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   d2 = 9
   d4 = 4
   plot()
   circle(sqrt(d1*d2), d1/2, d1/2, :blue)
   circle(0, d2/2, d2/2)
   circle(sqrt(d2*d3), d3/2, d3/2, :green)
   circle(sqrt(d2*d3) + sqrt(d3*d4), d4/2, d4/2, :magenta)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(sqrt(d1*d2), d1/2, " 甲円", :blue, :left, :vcenter)
       point(0, d2/2, " 乙円", :red, :left, :vcenter)
       point(sqrt(d2*d3), d3/2, " 丙円", :green, :left, :vcenter)
       point(sqrt(d2*d3) + sqrt(d3*d4), d4/2, " 丁円", :magenta, :left, :vcenter)
   end  
end;

draw(25, 1, true)