上下反転した数字表示器
締め切りが 2017/04/11 10:00 AM なので,その 1 分後に投稿されるように予約
設問
図のような7セグメントディスプレイを使った数字表示器があります。
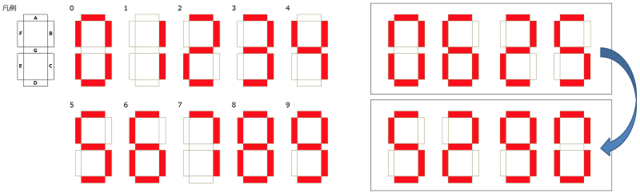
この数字表示器を上下逆さに置いたとき、例えば「0625」は「5290」と読むことができます。
逆さに置いたときに対応する数字は以下のようになります。
0 0
1 1
2 2
5 5
6 9
8 8
(「1」は反転すると位置がずれますが、「1」として読み取ることが可能なものとします。)
n 桁を表示できる数字表示器を通常の置き方で置いた時よりも、上下逆さに置いた場合の方が大きな値として読み取ることができるものが何通りあるかを求めるプログラムを作成してください。
例えば、n = 2のとき、以下の21通りがあります。
01, 02, 05, 06, 08, 09, 12, 15, 16, 18, 19, 25, 26, 28, 29, 56, 58, 59, 66, 68, 86
標準入力から自然数 n が与えられますので、パターン数を標準出力に出力してください。
なお、n は最大で20とします。
【入出力サンプル】
標準入力
2
標準出力
21
=============================================
何の策略もないシンプルなプログラムを書いて,n が小さいときの解を求め,既知の数列であるかまたは漸化式を見いだせるかという,いつもの戦略。
f = function(n) {
d = c(0, 1, 2, 5, 6, 8, 9)
d.rev = c(0, 1, 2, 5, 9, 8, 6)
g = function(m) {
x = x.rev = integer(n)
n1 = n+1
for (j in seq_len(n)) {
k = m %% 7 +1
x[n1-j] = d[k]
x.rev[j] = d.rev[k]
m = m %/% 7
}
as.numeric(paste(x.rev, collapse="")) > as.numeric(paste(x, collapse=""))
}
count = 0
for (i in seq_len(7^n)-1) {
count = count+g(i)
}
cat(count, "\n")
}
このプログラムでは,f(7) = 410914 を計算するのに 40 秒近く掛かるが,とにかく
n f(n)
1 1
2 21
3 154
4 1176
5 8281
6 58653
7 410914
が得られる。
漸化式に用いる項数を2,3,4...(1 項では明らかにむり) として,重回帰モデルを考える
n x1 x2 x3 x4
1 1 21 154 1176
2 21 154 1176 8281
3 154 1176 8281 58653
4 1176 8281 58653 410914
で,
> a = lm(x4 ~ x1+x2+x3, d)
> summary(a)
Call:
lm(formula = x4 ~ x1 + x2 + x3, data = d)
Residuals:
ALL 4 residuals are 0: no residual degrees of freedom!
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0 NA NA NA
x1 -49 NA NA NA
x2 7 NA NA NA
x3 7 NA NA NA
Residual standard error: NaN on 0 degrees of freedom
Multiple R-squared: 1, Adjusted R-squared: NaN
F-statistic: NaN on 3 and 0 DF, p-value: NA
> predict(a)
1 2 3 4
1176 8281 58653 410914
となり,漸化式,a[1] = 1, a[2] = 21, a[3] = 154 で,n >= 4 は,a[n] = 7*a[n-1] +7*a[n-2]-49*a[n-3]
これに基づいて,
f = function(n) {
x = numeric(20)
x[1:3] = c(1, 21, 154)
if (n >= 4) {
for (i in 4:n) {
x[i] = 7*(x[i-1]+x[i-2])-49*x[i-3]
}
}
options(scipen=100)
cat(x[n])
}
system.time(f(20)) # 39896133007568376 0.001seq.




























※コメント投稿者のブログIDはブログ作成者のみに通知されます