算額（その1515）

算額（その1515）

八十三 岩手県一関市藤沢町保呂羽字二本柳 保呂羽神社 明治26年(1893)
山村善夫：現存 岩手の算額，昭和52年1月30日，熊谷印刷，盛岡市.
http://www.wasan.jp/yamamura/yamamura.html

今有如図 03078
https://w.atwiki.jp/sangaku/pages/313.html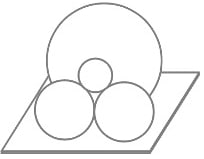

キーワード：球4個
#Julia, #SymPy, #算額, #和算

台の上に甲球，乙球，丙球が載っている。甲球，乙球の直径及び「高」が与えられたとき，丙球の直径を求める術を述べよ。

注：意味のある「高」は唯一，盤面から乙球の天辺までの距離（高さ）である。

甲球の半径と中心座標を r1, (0, 0, r1)
乙球の半径と中心座標を r2, (x2, r2, r2)
丙球の半径と中心座標を r3, (x3, 0, z3)
「高」を h とおき，以下の連立方程式を解く。

using SymPy
@syms r1, r2, x2, r3, x3, z3, h
eq1 = x3^2 + (z3 - r1)^2 - (r1 + r3)^2
eq2 = x2^2 + r2^2 + (r2 - r1)^2 - (r1 + r2)^2
eq3 = (x3 - x2)^2 + r2^2 + (z3 - r2)^2 - (r2 + r3)^2
eq4 = z3 + r3 - h;

res = solve([eq1, eq2, eq3, eq4], (r3, x2, x3, z3))[2]  # 2 of 2

    (r1*(h^2*r1 + 2*h^2*r2 - 4*h*r1*r2 - 2*h*r2^2 + 4*r1*r2^2)/(2*h*r2*(4*r1 - r2)), r2*sqrt(1/(r2*(4*r1 - r2)))*(4*r1 - r2), sqrt(1/(r2*(4*r1 - r2)))*(h*r1 - h*r2 + 2*r1*r2), (-h^2*r1^2/2 + 3*h^2*r1*r2 - h^2*r2^2 + 2*h*r1^2*r2 + h*r1*r2^2 - 2*r1^2*r2^2)/(h*r2*(4*r1 - r2)))

# r3: 丙球の半径
res[1]

甲球，乙球の半径が 5, 4, 高さが 12 の場合，各パラメータは以下のとおりである。

res[1](r1 => 5, r2 => 4, h => 12).evalf() |> println
res[2](r1 => 5, r2 => 4, h => 12).evalf() |> println
res[3](r1 => 5, r2 => 4, h => 12).evalf() |> println
res[4](r1 => 5, r2 => 4, h => 12).evalf() |> println

    2.76041666666667
    8.00000000000000
    6.50000000000000
    9.23958333333333