2021 年日本数学オリンピック予選 問題 1, 2, 3
https://www.imojp.org/archive/mo2021/jmo2021/problems/jmo31yq.html
Q1.
互いに素な正の整数 m, n が m + n = 90 をみたすとき,積 mn としてありうる,最大の値を求めよ。
value = 0
mn = ()
for m = 1:45
n = 90 - m
gcd(m, n) == 1 && (value = max(value, m * n); mn = (m, n))
end
println("mn = $value, (m, n) = $mn") # 2021
mn = 2021, (m, n) = (43, 47)
Q2.
下図のような正十角形がある。全体の面積が 1 のとき,斜線部(濃い青色を付けた2つの部分)の面積を求めよ。
using Plots
pyplot(label="")
x = zeros(10)
y = zeros(10)
for i = 1:10
y[i], x[i] = sincosd(i*36)
end
δ = [1, 1, -1, -1, -1, -1, -1, 1, 1, 1].*0.1
plot(x, y, seriestype=:shape, fillcolor=false, tickfontsize=12,
aspect_ratio=1, xlims=(-1.2, 1.2))
plot!(x[[1, 2, 3, 6]], y[[1, 2, 3, 6]], seriestype=:shape, fillcolor=:blue)
plot!(x[[1, 9, 10]], y[[1, 9, 10]], seriestype=:shape, fillcolor=:blue)
plot!(x[[4, 5, 6]], y[[4, 5, 6]], seriestype=:shape, fillcolor=:blue, alpha=0.3)
annotate!(x .+ δ, y, Char.(65:74))
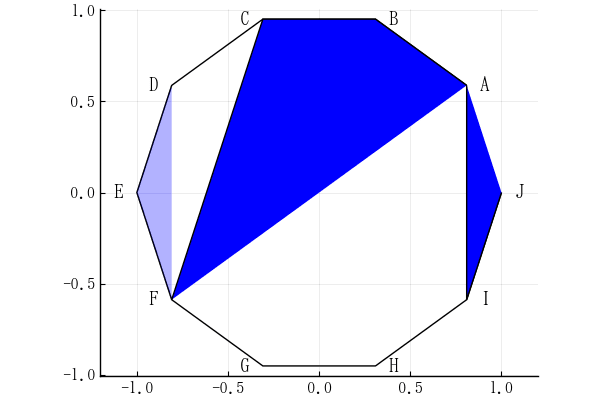
三角形 AIJ を 三角形 DEF の位置に移動すれば,色の付いた面積は,正十角形の面積の半分から,三角形CDF の面積を除いたものである。 正十角形の頂点 A, B, ..., J の x, y 座標は ベクトル x, y に入っている。 線分 CF, DF の長さ,∠DFC = θ を求める。
CF = sqrt((x[3] - x[6])^2 + (y[3] - y[6])^2)
1.6180339887498947
DF = sqrt((x[4] - x[6])^2 + (y[4] - y[6])^2)
DF = y[4] - y[6]
1.1755705045849463
θ = 90 - atand((y[3] - y[6]) / (x[3] - x[6]))
18.0
よって,三角形 EFC の面積 s は
s = CF * DF * sind(θ)
0.5877852522924731
正十角形の面積 S は 10sind(θ)
S = 10sind(36)
5.877852522924732
よって,色を付けた部分の面積は
S/2 - s
2.3511410091698925
S = 1 とすると,
(S/2 - s) / S
0.39999999999999997
別解
多角形の面積を求める関数を定義していくつかの部分に分けて面積を求めてみよう。
n 多角形(当然三角形も)の頂点座標を反時計回りで n×2 行列で用意して関数を呼ぶ。
function area(xy)
x = xy[:, 1]
-sum((vcat(x[2:end], x[1]) - vcat(x[end], x[1:end-1])) .* xy[:, 2]) / 2
end
area (generic function with 1 method)
AIJ = area([x[1] y[1]; x[9] y[9]; x[10] y[10]])
0.11225699414489633
ABCF = area([x[1] y[1]; x[2] y[2]; x[3] y[3]; x[6] y[6]])
1.06331351044005
ABCDEF = 10area([0 0; x[1] y[1]; x[2] y[2]])
2.938926261462366
(AIJ + ABCF) / ABCDEF
0.39999999999999997
面白い(?)のは三角形 BCF の面積が正十角形の 1/10 であること。
BCF = area([x[3] y[3]; x[4] y[4]; x[6] y[6]])
0.29389262614623657
以下の図で,三角形 CDF と三角形 CDO の面積が等しいから,最初の図の色の付いた部分は全体の 4/10。
plot!([x[3], x[4], 0], [y[3], y[4], 0], seriestype=:shape, fillcolor=:green, alpha=0.3)
annotate!(0.05, -0.05, "O")
これに気づけば,なにもコンピュータなんか使わなくても答えは出る。
Q3.
AB = AC なる二等辺三角形 ABC の内部に点 P をとり,P から辺 BC,CA,AB におろした垂線の足をそれぞれ D,E,F とする。BD = 9,CD = 5,PE = 2,PF = 5 のとき,辺 AB の長さを求めよ。ただし,XY で線分 XY の長さを表すものとする。

P を通り,BC に平行な直線を描き,AB,AC との交点を Q, R とする。 ⊿FQP ∽ ⊿ ERP ゆえ,QP:PR = 5:2
# QP を求める
using SymPy
@syms QP PR
eq1 = Eq(2QP, 5PR)
eq2 = Eq(QP - PR, 4)
s1 = solve([eq1, eq2])
Dict{Any, Any} with 2 entries:
PR => 8/3
QP => 20/3
FQ を求める
FP = 5
QP = s1[QP]
FQ = sqrt(QP^2 - FP^2)
println(string(FQ))
5*sqrt(7)/3
A から底辺におろした垂線の足を O とすれば, ⊿FQP ∽ ⊿OBA より,FQ:PQ = BO:AB
AB を求める
BO = 7
AB =QP * BO / FQ
println(string(AB))
4*sqrt(7)
これが答えだ。






















