(2)候補数を消去する
⑬「Sashimi Fish」の成立を調べる
「Sashime Fish」なる言葉、初めて聞く言葉だと思います。マーちゃんも、最近学んだ「手筋」です。ミシチャンさんのホームページで初めて見ました。実はこのブログを書くに当たって、実に多くのことを教えていただき、又参考とさせて頂いています。
ホームページアドレスは以下の通りです。
http://www.geocities.jp/master_mishichan/
「複数の候補数に渡って調べる」範疇で「XY-wing」や「浜田ロジック」の成立等を調べてきましたが、ここからは「ある特定の候補数について調べる」に逆戻りします。「単独の候補数」から「複数の候補数」と言う流れに反しますが、ここからの話はより難易度が増しますから、その面ではより後半に登場させるので良いのではないかと思います。まず「X-wing」の証明の見直しから話を始めます。図1を見てください。
図1
候補数を例えば5としましょう。図1でa行には2列と8列にのみ候補数5が存在します。その2つをAとaと表しています。この様に、あるユニット内に候補数が2個しか存在しないとき”対をなす”と呼べばa行でAとaは対をなしています。
又g行でも候補数5は対をなして存在し、Bとbです。このAとBが同一列の2列に存在し、aとbが同一列の8列の存在しますから、「X-wing」が成立し2列(水色印のマス)と8列(黄色印マス)から候補数5を消去出来るのでした。
その理由を以前とは異なる理屈で説明します。
図2
図2でもし黄色印マスで5が確定したとしましょう。具体的にi8=5とします。ここが5と確定すれば8列にもはや5は存在できませんから、aとbは消去されます。
図3
図3でaが消えましたから、aと対をなすAは必ず成立。bも消えましたから、bと対を成すBも必ず成立。同一列内で、AとBが成立するのは矛盾である。だから黄色印マスには5は存在し得ない、となります(部分的に背理法を用いています)
水色印マスには5が存在し得ない事も同様な理屈ですから、省略しますが、ここで重要な事は、aとbを見る事が出来るマスには5は存在し得ないと言う事実です。
この理屈は次のような場面で応用が利きそうです。
図4
候補数5は図4の様に存在してるとしましょう。この配置では「X-wing」は成立していません。しかし、先に述べた理屈に準じて、aとbの両方を見れる位置に存在するマスがあれば、そのマスの候補数は、図2・図3のcと同じ働きをするはずです。具体的には図5を見てください。
図5
図5で黄色印マスはaとbの両方を見る事が出来ます。(前に書いた事のおさらいですが、黄色印マスはaと同じユニットに属し、bとも同一のユニットに属します)
この黄色印マスで5が確定するとaとbは成立しなくなり、云わばその反動としてAとBが成立し、矛盾が起こります。だから黄色印マスに5は存在しえず、ここから候補数5を消去できます。
以上の一連の手筋を「Sashimi Fish」と呼ぶそうです。この観点に立つとまだまだ候補数を消去出来る「手筋」がありそうです。次々回ブログでは「Finned Fish」を紹介し、その先ではマーちゃんが気が付いた「手筋」を紹介します。その前に問題を一題。
例題 図6の局面で「Sashimi Fish」が成立しています。それを指摘し、局面を一歩先に進めて下さい(問題は、ミシチャンさんのブログから引用しています)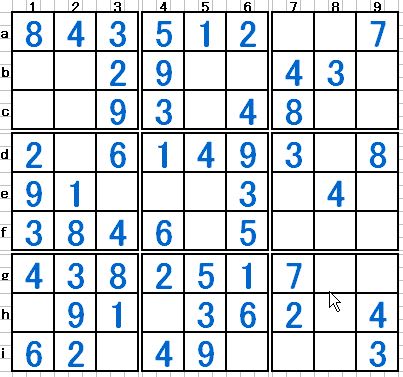
図6









