(2)候補数を消去する
⑮その他の手筋
例えば「XYZ-wing」等まだまだ多くの手筋があります。ただマーちゃんはその辺の部分は未だ不勉強で、具体的題材の収集も出来ていません。「どんな超難問数独でも解決出来る方法を解説します」が看板倒れに終わりそうですが、ただ、今までの説明で現在市販されてい超難問は殆ど解決できると考えています。「二コリ社」の「激辛数独」も「世界文化社」の「難問ナンプレ」や「ナンプレ超上級編」も解決します。挑戦してみてください。
ここで紹介が出来ず、ミシチャンさんのホームページに登場するような手筋が問題に組み込まれていれば解けないこともあるかと思いますが、ご容赦下さい。それに新たに手筋が発見される事もあります。ナンプレ・数独の世界は日進月歩しています。いずれ又知識を整理してからこの続きを書き出したいと思いますが、今日でとりあえず終了します。
長らく読み続けられた方がいらっしゃいましたら心からお礼申し上げます。マーちゃんは、東京散歩とか、再度の百名山、江戸時代の数学(和算)などに興味があります。身辺雑記も含め、今後はそれらについてのブログを書きますので、宜しければそちらをお読み下さい。(7月22日以降)
最後の幾つかはマーちゃんが気が付いた事柄です。図1をご覧下さい。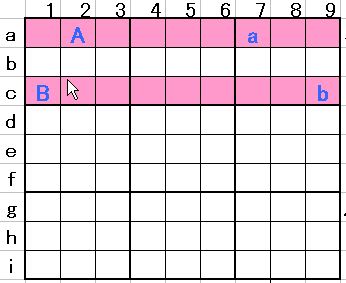
図1
「X-wing」が「候補数が二つのだけの行が2つあり、その候補数が同じ列の上にあるならば、その列にはその候補数はそれ以外には存在しない」と言うものでした。(行と列を入れ替える事可能)
この「X-wing」の手筋の後半部分を書き換えるとどうなるでしょう。
仮定は「候補数が二つだけの行が2つあり、その候補数が同じブロック内にあるならば・・・」です。どんな結論が待っているでしょうか?
候補数5についての配置が図1の様に、a行にはAとa、c行にはBとbとします。この時AとBが同じブロックに、aとbも同じブロックに属しているという仮定です。このときにも消去出来る候補数があります。図2を見て下さい。
図2
例えば図2で黄色印マスのどれかが5で確定したとすると、aとbは消去され、AとBが残りこれは困ります。(具体的事例を前提にしての話ではありませんので、この様な仮定がありえるのか否か検討していません。黄色印マスでの5の確定がAとBの存在に影響を与えない、とします)
謂わば「X-wing」の拡張は次の様にも言い換えられます。
図3
図3で「候補数が二つだけのブロックが2つあり、その候補数が同じ行の上にあるならば・・・」。さてこのときの結論はどうなるでしょう。図4を見てください。
図4
例えば黄色印マスのいずれかが5で確定すれば、a、bは消去され、a行にAとBが残ります。これは困ります。だから黄色印マスに5は存在し得ず、こから候補数5を消去出来ます。
図5からは「Sashimi Fish」や「Finned Fish」の拡張を考えますです。
ミシチャンさんのホームページを参考にさせていただきましたが、理屈はマーちゃん流です。図5を見て下さい。
図5
図5は「Sword Fish」が成立しています。その時黄色印マスに5は入りません。理屈を復習します。
もし黄色印マスに5が入ればa’、b’、c’は消去され、Aa, Bb , Ccが残されます。この形覚えておくと有効だと思います。あってはならない配置なのです。(”困った配置”と呼ぶ事にします。仮にAa, Bbでの「X-wing」が成立と見立てればCcが消えてしまいh行に5は存在しえなくなってしまいます)これが「Sword Fish」で候補数を消去出きる理屈です。この理屈は次のような局面でも使えます。
図6
「Sashimi Fish」の「Sword Fish」版です。b行、e行、h行に候補数は3個(2個でも可)で、候補数が上記の様に配置されているとします。このとき候補数5を消去出来るマスがあります。
図7
図7でa’、b’、c’の3つを見る事の出来るマス、すなわち黄色印マスから候補数5を消去出来ます。(理由は、ここで5が成立すると、a’、b’、c’が消去され、”困った配置”となってしまいます。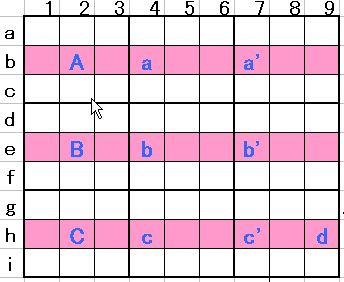
図8
図8は「Finned Fish」の「Sword Fish」版です。
図9
図9の黄色印マスから5が消去出来ます。
黄色印マスで5が確定すると、a’、b’、c’、dが消去され、Aa, Bb, Cc の”困った配置”になってしまうからです。









