(2)候補数を消去する
⑭「Finned Fish」の成立を調べる
図1を見てください。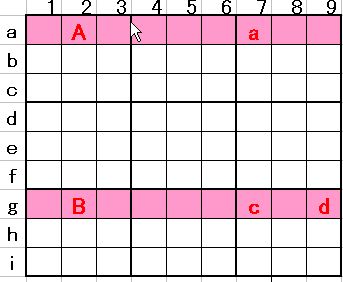
図1
図1も「Sashimi Fish」と同じように、「X-wing」が成立しそうで、僅かなところで「X-wing」は成立していません。「Sashimi Fish」が、候補数4個で成立した手筋に対して、上記の場合はg行の候補数が3個。この局面で消去出来そうな候補数は無い様に思えます。ところがあるのです。
先ず候補数の配置から説明します。「Sashimi Fish」のとき同様、候補数5について、以下の様になっているとします。
a行はAとaが対をなしています。
g行に候補数は3個あり、それらの記号は、対をなすわけではないのでBに対してのbを用いないで、c、dで表しています。dを取り去れば「X-wing」成立、言い方を変えれば「X-wing」にdが追加されている配置です。この時,候補数5は消去出来るマスはあるでしょうか?暫く考えた後に図2をご覧下さい。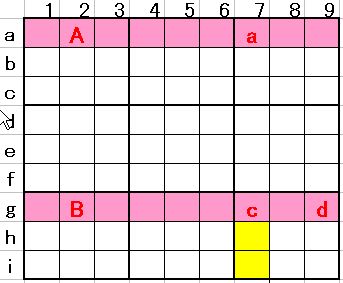
図2
上図の黄色印マスから候補数5を消去出来ます。理由は簡単です。この黄色印マスで5が成立すれば、a、c、dは全て消去され、その結果AとBが成立する事になり、これは困ります。だから黄色印マスから候補数5を消去出来る分けです。
この一連の理屈を「Finned Fish」と呼ぶそうです。
finned を英和辞書で調べると、「ひれをもった」とか「ひれの・・」とあります。「X-wing」を魚に見立て、それにひれが付いたと言う意味でしょうか。或いは”ひれの付いた魚”と言う風に解釈すれば、このネイミングが理解可能です。
今後のブログで展開しようとする理屈を理解していただく観点を紹介すれば、a、c、dの全てを見る事の出来る地点(=マス)で候補数5は不成立です。AとBが残るような状況はあってはならないとの判断から、消去マスを見つけるわけです。例えば図3をご覧下さい。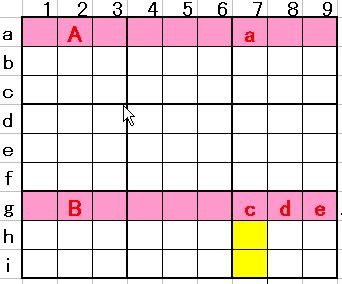
図3
図3は「Sashimi Fish」でも「Finned Fish」でもありません。敢えて言えば、dを取り去れば「Finned Fish」、cとeを取り去れば「Sashimi Fish」で、「Finned Fish」+「Sashimi fish」の様な状態です。「手筋」ではありませんが、このa、c、d、eを見る事が出来るマスでは5は不成立のはずです。黄色印マスはこれらをすべて見渡せます。だから黄色印マスから5を消去出来ます。
この手筋発見でも2つのライン、AaラインとABラインが直角をなす事の発見に神経を集中することで、この手筋発見が可能となると思います。 次のような観点からも発見への糸口が開けると思うのです。
それは対をなすラインAaラインに平行で2個又は3個の点(=マス)を持つラインの存在発見に精神を集中させる、と言う観点です。
例題 次の局面で「Finned Fish」を発見してください。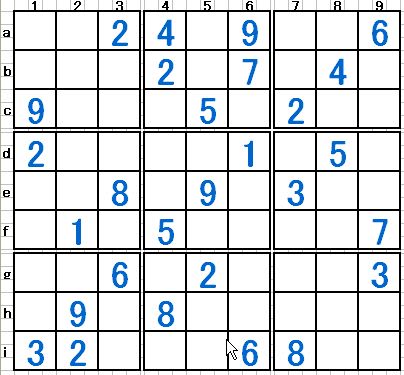
図4
解説は次回のブログで。
(2)候補数を消去する
⑬「Sashimi Fish」の成立を調べる
それにしてもこの手筋に妙な名前をつけたものです。多くの手筋に「Fish」が付けられる理由、面白いと思いますが、私には謎です。一体誰がいつ頃、これらの手筋を発見したのか興味が湧きます。外国の文献を読めば少しは様子が分かるかもしれませんが・・・。図1は前回のブログでの問題の再掲です。
図1
候補数の状況を明らかにして図2です。
図2
マーちゃんは1~9の順にオセロ石を配置して調べます。
そのときに、”対をなす”二つのマス、云わば2点を結ぶ線分が2本あり、直角をなす場合を捜すのに精神を集中させます。
候補数7の配置がその様になっていました。図3を見てください。
図3
”対をなす”マスを結ぶ線分は、e3ーe4 ラインが一本、e4-h4 のラインがもう一本、この2本が直角を形成しています。
黄色印マス4個が「Sashimi Fish」形成です。このときマスh4とマスi3の両方を見るマスh1(水色印マス)から7が消去出来ます。h1=7が成立すれば、i3≠7、h4≠7。だからe3=7かつe4=7 が成立して困ります。∴h1=5 です。
ペア数{57}の奇数個の連鎖 h1-i3-e3 で「浜田ロジック」が成立しh1=5、i3=7、e3=5 と解く事も出来ます。
その後は問題なく図4の最終局面に到達です。
図4









