ダメ出し：小細工せずに素直に（あるいは，効果を確かめてから）

「kingqwertの覚書」 の
http://d.hatena.ne.jp/kingqwert/
2012-08-22 の項
http://d.hatena.ne.jp/kingqwert/20120822

「リサイクル規則をうまく使う方法」を挙げてあるが，そんなに良い方法ではない。内部では結局の所リサイクル処理をしているので，1:(n%/%2)*2 のように選択する添え字ベクトルを指定してやるのと同等の速度である。むしろ，一番最後の例のように，添え字が整数ベクトルになるようにすれば，一番速い。

> n <- 10000000L
> a <- rnorm(n)
>
> invisible(gc()); invisible(gc()); system.time({
+     x <- a[seq_along(a) %% 2 == 0]
+ })
   ユーザ   システム       経過  
     0.363      0.010      0.371
> invisible(gc()); invisible(gc()); system.time({
+     y <- a[!(seq_along(a) %% 2)]
+ })
   ユーザ   システム       経過  
     0.345      0.000      0.344
> invisible(gc()); invisible(gc()); system.time({
+     z <- a[c(FALSE,TRUE)]
+ })
   ユーザ   システム       経過  
     0.076      0.001      0.077
> invisible(gc()); invisible(gc()); system.time({
+     u <- a[1:(n%/%2)*2]
+ })
   ユーザ   システム       経過  
     0.063      0.001      0.063
> invisible(gc()); invisible(gc()); system.time({
+     v <- a[1:(n%/%2)*2L]                        # 最速！！
+ })
   ユーザ   システム       経過  
     0.048      0.000      0.048

> all(x == y)
[1] TRUE
> all(x == z)
[1] TRUE
> all(x == u)
[1] TRUE
> all(x == v)
[1] TRUE

ダメ出し：もう何回も書いたけど...

「高校数学でわかる統計学」の「第1章　サイは投げられた！（期待値と分散）」 において，

乱数は纏めて発生させる。そうすれば for ループを使う必要もない。
両方併せると，実行時間に大きな違いが出る（もっとも，100000 × 2 個発生させて 1 秒なんだから，時間が問題なのではない（

> system.time({
+ n <- 100000
+ x <- numeric(n)
+ for (i in 1:n) {
+  x[i] <- sum(sample(x=1:6, size=2, replace=TRUE, prob=rep(1, 6)))
+ }
+ barplot(table(x) / n, ylim=c(0, 0.2))
+ })
   ユーザ   システム       経過  
     1.302      0.017      1.318

> system.time({
+ n <- 100000
+ d <- matrix(sample(1:6, 2*n, replace=TRUE), 2)
+ x <- colSums(d)
+ barplot(table(x)/n, ylim=c(0, 0.2))
+ })
   ユーザ   システム       経過  
     0.128      0.003      0.136

ダメ出し：二項分布の確率分布図

「楽しい　統計学セミナー　- 証拠を科学する方法 -」の「第3講」 において

サイコロを6回振って，6の目が出る「確率分布図」を描いてみる．
　　：
X軸のラベルを確率変数Xと合わせることができない・・・　といっているが...

この項は，前の記事に既に解があるが...

x <- numeric(7)
 for (i in 0:6) {
 x[i +1 ] <- choose(6, i) * (1 / 6)^(i) * (5 / 6)^(6 - i)
}
plot(x, type="l", xaxt ="n", xlab="X", ylab="probability")
axis(side=1, at=0:6)

X 軸のラベルを確率変数 X と合わせるには，axis(side=1, at=1:7, labels=0:6) とすればよいだけ。
ここでも，実際の x の添え字は 0～6 だが，R では 1 ～ 7 になっているという食い違いを，ちゃんと吸収できていないことが原因（前の記事での指摘通り）。

度数分布を折れ線で描く（度数多角形という）ということもあるが，離散変数の分布は barplot 関数で描く方がよい。
R のbarplot は，横軸のラベルを描いてくれないので自分で描く。
確率分布関数として dbinom を使うということも，以前指摘したとおり。

barplot(dbinom(0:6, 6, 1/6), ylab="Probability", xlab="x")
axis(1, 0:6*1.2+0.6, 0:6)

ダメ出し：添え字はそのまま使う

「楽しい　統計学セミナー　- 証拠を科学する方法 -」の「第2講」 において

試行回数 N=10～100 に対する二項分布の確率関数を

x <- numeric(91)
for (i in 10:100) {
 x[i - 9] <- choose(i, 3) * (1/10)^(3) * (1- (1/10))^(i - 3)
}
plot(x)
abline(v = 20.5, col="blue")

のように，書いている。10 ~ 100 を添え字として 1 ～ 91 を使おうということで numeric(91) とか for (i in 10:100) とか x[i - 9] とか，様々な注意が必要。しかし，このようなことはちょっと油断するとバグの混入原因。縦軸（確率）を納める変数名が x なのも混乱を増幅するが。

実際，掲載されたプログラムが
for (i in 10:91) {
 x[i - 9] <- > for (i in 10:100) {
となっていたり，確率が最大になる index の値を図に示すと，index=20, 21 のときに最大になるというように見えるが，求める数値は 29 と 30 なのだ，のように，ぼろが出る。

添え字は，0 やマイナスの値にならない限りそのまま使う方がよい。

y <- numeric(100)
n <- 10:100
for (i in n) {
 y[i] <- choose(i, 3) * (1/10)^(3) * (1- (1/10))^(i - 3)
}
plot(n, y[n])
abline(v = 29.5, col="blue")

なお，二項分布の確率関数は dbinom で計算できる

> x <- 10:100
> y <- dbinom(3, x, 1/10)
> plot(x, y, type="l", ylim=c(0, 0.25))
> (index <- which.max(y))
[1] 20
> abline(v = x[index] + 0.5, col="blue")
> (max.value <- y[index])
[1] 0.2360879322323426

難しく考えない

「楽しい　統計学セミナー　- 証拠を科学する方法 -」の「第1講」 において，

当初目指していた「（問題）サイコロを6回投げたとき，6の目が1回だけ出る確率は？ 」であるが，これは，生起確率が 1/6 である事象が 6 回の施行中に 1 回だけ起きるということで，それは二項分布だ。
Prob = dbinom(1, 6, 1/6) = 0.4018776 で，これを確かめるシミュレーションプログラムは，前のプログラムをちょっと変更すると得られる。
なお，水平線を引くのは abline(h = value, ...) である。

system.time({
set.seed(12345)
n <- 10000
x <- matrix(sample(0:1, 6*n, replace=TRUE, prob=c(5/6, 1/6)), 6)
y <- cumsum(colSums(x)==1)/1:n
plot(y, type="l")
abline(h = dbinom(1, 6, 1/6), col="red")
})

barplot(dbinom(0:6, 6, 1/6), ylab="Probability", xlab="x")
axis(1, 0:6*1.2+0.6, 0:6)

シミュレーションの仕方

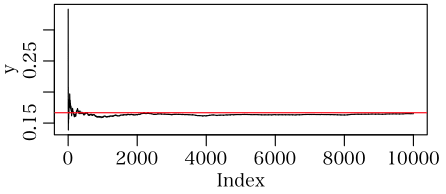
「楽しい　統計学セミナー　- 証拠を科学する方法 -」の「第1講」 において，シミュレーションプログラムが掲示されているが

system.time({
set.seed(12345) # 乱数の初期値を設定しておこう
n <- 10000      # プログラムの中で何回も出てくる数値は変数に代入しておいて使おう（一箇所で変更できる）

# for (i in 1:n) { # 等差数列を作るというのだが...
#  x[i] <- 6*i
# }
x <- 1:n*6         # ベクトル演算はこんなときにも使える (1:n)*6 と書くかは，好みの問題

y <- numeric(n)    # １～n回の試行を格納するための変数を確保．

for (i in 1:n) {
  a <-sample(x=1:6, size=x[i], replace=TRUE, prob=c(rep(1/6, 6)))
# y[i] <- (sum(a[a == 1])) / x[i] # 足してデータの個数で割るというのは...
  y[i] <- mean(a == 1)            # 平均値を求めるということ
}                                 # ちなみに，(a[a == 1]) は冗長

plot(y, type="l")
abline(a = 1 / 6, b = 0, col="red")
})

このプログラムでは，「6 回サイコロを振る」ということを，毎回 1～x[i] 繰り返す。
もう一つの考え方は，1 ~ n 回繰り返し，その途中経過を見るということでもよい。もっとも，こちらの考え方では k 回の時点での結果は k-1 回までの結果に従属であるということではあるが（前述の方法では，各回の結果は独立）。

もう一つのポイントは，1の目が出るということに注目するのであるから，2～6の目が出ることをシミュレーションする必要はないということ。つまり 1 とそれ以外の目が 1/6, 5/6 で出るというシミュレーションをすればよいということ。TRUE/FALSE や，成功回数を数えるときに sum が直接使えるということを考えれば，1 の目がでることを 1，それ以外の目が出ることを 0 で表すとよい。つまり n 回の試行結果は x <- sample(0:1, n, replace=TRUE, prob=c(5/6, 1/6)) で得られ，k 回目までの成功数は cumsum(x) で得られ，成功率は cumsum(x)/1:n で得られることになる。ということで，纏めると

system.time({
set.seed(12345)
n <- 10000
x <- matrix(sample(0:1, 6*n, replace=TRUE, prob=c(5/6, 1/6)), 6)
y <- cumsum(colSums(x))/6/1:n
plot(y, type="l")
abline(a = 1 / 6, b = 0, col="red")
})

前のプログラムの実行時間は
   ユーザ   システム       経過  
    15.418      2.327     17.636

後ろのプログラムの実行時間は
   ユーザ   システム       経過  
     0.136      0.004      0.155

ダメ出し：なんでそうなるの?

久保さんのページ 2012/08/21 で，研究会の発表で使ったスライドが掲示されているけど，Z得点は，(観察値-μ)/σ だと思うよ。逆にしたら符号が逆になる。