ルーカス数列

ルーカス数列は，フィボナッチ数列から生成される。

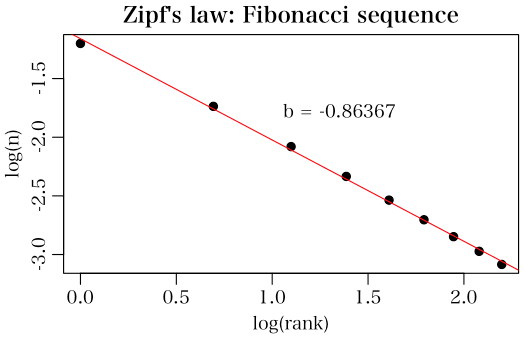
Fibonacci numbers are define by: Fn=Fn-1 + Fn-2

Lucas numbers are define by: Ln=Fn + 2Fn-1

フィボナッチ数列のときと同じようにして，

import scipy as sp

n = 100000
tbl = sp.zeros(10, dtype=int)
a, b = 1, 3
tbl[1], tbl[3] = 1, 1
for i in range(2, n):
  a, b = b, a+b
  tbl[int(str(b)[0])] += 1
print(tbl[1:])

これによって，先頭桁が 1 ~ 9 である項数が以下のようであることが分かる。

[30104 17609 12494  9691  7919  6695  5799  5115  4574]

フィボナッチ数列の場合は

[30103 17610 12494  9690  7918  6695  5798  5117  4575]

だったので，ほとんど同じである。両方ともベンフォードの法則にしたがうといえる。
それにしても，実に良く一致している。

Zipf の法則

「素数の先頭桁の数字の分布」で，「拡張されたベンフォードの法則」というのが出てきた。「拡張されたジップの法則（Zipf's law）」というのは知っているが「拡張されたベンフォードの法則」というのは，この論文ではじめて知った。

「ベンフォードの法則」は「ジップの法則の」特殊例。ジップの法則は出現頻度の大きさに応じて順位を r とすると，r 番目の頻度（度数）n は，a * r ^ b にしたがうというもの。b = -1 の場合が「ジップの法則」，b ≠ -1 の場合が「拡張されたジップの法則」。b = -1 のとき，一番大きいものが 100 なら，2 番目に大きいものは 100 * 2 ^(-1) = 50，3 番目に大きいものは 100 * 3 ^(-1) =33，4 番目に大きいものは 100 * 4 ^(-1) ＝ 25 などとなる。

n = a * r ^ b の両辺の対数をとると，log(n) = log(a) + b * log(r) となるので，n, r の対数をとって直線回帰を行うと，「回帰直線の傾き」が b である。a は一番多いものの度数（頻度）の推定値になる。

ベンフォードの法則によくあてはまっていた，フィボナッチ数列については以下の図のようになるので，「拡張されたジップの法則」にしたがっていることが分かる。

階乗についてはベンフォードの法則から若干外れていた。下図のようになるので，やはり少しずれはあるが「拡張されたジップの法則」にしたがっていることが分かる。

[1, 10^10] の範囲内の素数の先頭桁の数字の分布は「拡張されたベンフォードの法則」にしたがうとされていた。

図に示すと以下のようになり，やはり「拡張されたジップの法則」にしたがっていることが分るが，b の値は大きく違う事に注意。b が 0 のときにはこの直線は x 軸に平行になるわけで，度数は全て等しくなる（一様分布になる）。b が -0..03942 ということは，かなり一様分布に近づいていることが分かる。

ちなみに [1, 10^7] の範囲内の素数については b = -0.05835 である。

なお，[1, 10^6] の範囲だと，「拡張されたジップの法則（拡張されたベンフォードの法則）」からのズレが相当大きい。

それより狭い範囲では推して知るべし。