やあ,ジュン。元気かい?
元気だよ。
前に,ポケモン Go のことで教えてもらったけど,またいいかな?
いいよ。でも,ポケモン Go に興味がない人にも分かるような例で説明してくれる?
そうか〜。うんとね。あ,そうそう。野球にたとえるとこんなになるかな。「3 割バッターが,3 連続ヒットを打てるまでに何回打席に立たなければならないか」でいいかな。前に教えてもらった負の二項分布に似ている気もする。
ヒットを打ったら 1,打たなかったら 0 で表すと,打席の記録は 100110100111 のように最後の3桁が 111 になったら 3 連続ヒットを打ったということ。当然だけど,最後の 3 桁より左には 1 が 3 つ以上連続することはない。この例だと,12 打席目で 3 連続ヒットを達成ということだけど,確率変数 x は 3 連続ヒットまでの打席数として 9 と考えるほうがいいんだろうね。
そうだね。3 打席連続でヒットを打ったときは 111 で終わりなので,連続ヒットまでの打席数は 0 だから,そのほうが都合がいいよね。
打率を p としよう。x = 0 のときの確率はわかるよね。
それは,簡単。p * p* p = p^3 だね。p = 0.3 なら 0.0270 だ。
じゃあ,x = 1 のときは?
打席の記録は 0111 だね。初打席が 1 だと 1111 になるけど,4打席目はないので,x = 0 のときの話になる。
確率は,打席の記録が 0 のとき 0.7, 1 のとき 0.3 を順に掛けていけばよいから
0.7 * 0.3 * 0.3 * 0.3 = 0.7 * 0.3^3 = 0.0189 だ。
次は,x = 2 だけど,最後の5打席目を打つまでに 111 が出ないように注意しないといけないね。
打席の記録は 10111 か 00111 だから,それぞれの起きる確率は 0.7 * 0.3^4 = 0.00567,0.7^2 * 0.3^3 = 0.01323 で,併せて 0.0189。
x = 3 のときは,000111, 010111, 100111, 110111 の 4 通り。でも,0 と 1 の個数で整理して (0 の個数,1 の個数) のように表すと(3, 3) が 1 通り, (2, 4) が 2 通り, (1, 5) が 1 通りなので,確率は
(0.7^3 * 0.3^3) + 2*(0.7^2 * 0.3^4) + (0.7 * 0.3^5) = 0.0189 になるね。
x = 1, 2, 3 のどの場合も確率が 0.189 というのもおもしろいね。
これを x = 4, 5, ... と間違いなくやっていくのも大変なので,プログラムを書こう。途中に 111 がある場合を除いて勘定するために打席記録の最後が 0111 で終わるものだけを対象にする。
library(e1071)
f = function(k, p = 0.3) {
Z = NULL
b = bincombinations(k)
P = apply(b, 1, function(x) {
if (! grepl("111", paste(x, collapse=""))) {
ones = sum(x)
zeros = k-ones
Z <<- c(Z, ones)
p^(ones+3) * (1-p)^(zeros+1)
} else {
0
}
})
print(unname(table(Z)))
return(sum(P))
}
という関数を作って,以下のように実行する。
> p2 = numeric(11)
> for (i in 1:11) {
+ p2[i] = f(i)
+ }
[1] 1 1
[1] 1 2 1
[1] 1 3 3
[1] 1 4 6 2
[1] 1 5 10 7 1
[1] 1 6 15 16 6
[1] 1 7 21 30 19 3
[1] 1 8 28 50 45 16 1
[1] 1 9 36 77 90 51 10
[1] 1 10 45 112 161 126 45 4
[1] 1 11 55 156 266 266 141 30 1
これを図1のようにまとめる。
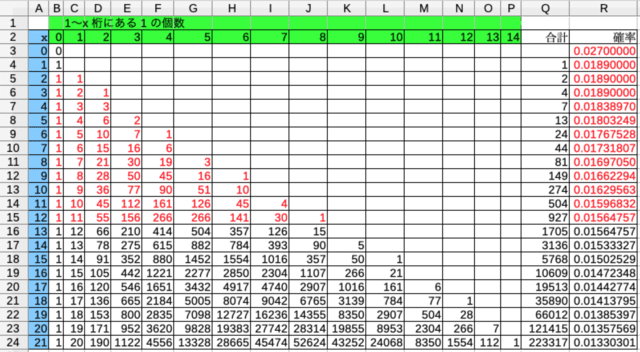
図の赤字で示したところが今求めた部分だ。「"111" より前の桁数」x が 2 〜 12 の場合について求めている。
それぞれの場合の確率も求められているよ。
> cbind(p2)
p2
[1,] 0.01890000
[2,] 0.01890000
[3,] 0.01838970
[4,] 0.01803249
[5,] 0.01767528
[6,] 0.01731807
[7,] 0.01697050
[8,] 0.01662969
[9,] 0.01629563
[10,] 0.01596832
[11,] 0.01564757
x = 3 の行を見れば,上に書いたのと同じになっているね。
のとき,1, 2, 1 とあるのは,1 が ない場合が 1 通り,1 個ある場合が 2 通り,2 個ある場合が 1 通りということである。最後の 0111 も併せて 0, 1 は (3, 3), (2, 4), (1,5) なので 確率は (0.7^3 * 0.3^3) + 2*(0.7^2 * 0.3^4) + (0.7 * 0.3^5) = 0.0189 となっている。
ちなみに,図1の合計欄の 1,2,4,7,13,24,44,81,... を「オンライン整数列大辞典」で検索してみると「Tribonacci numbers」というものであることが分かる。1+2+4 = 7, 2+4+7 = 13, ... だね。この表自体がある規則性を持っているという傍証だね。
x がもっと大きい範囲だとどうなるんだろうか。
x が大きくなると前述のプログラムでは計算できないので,図1の「1〜x 桁にある 1 の個数」が 4 の列の数列,1, 6, 19, 45, 90, 161, ... を「オンライン整数列大辞典」で検索してみると,「(1+x+x^2)^n を展開したときの x^4 の係数」というのがぴったり。5, 6 の列もみてみようか。
それぞれの列は x^0, x^1, x^2, ... の係数の数列になっているみたいだね。
n が大きくなると (1+x+x^2)^n を展開するのは大変じゃない?
真っ正直に展開する必要はないよ。係数だけを書き出すと
n = 1 のときは
1 1 1
n = 2 のときには
1 1 1
1 1 1
+ 1 1 1
===============
1 2 3 2 1
n = 3 のときには
1 2 3 2 1
1 2 3 2 1
+ 1 2 3 2 1
======================
1 3 6 7 6 3 1
とみたいに,単純に 1 桁ずつずらして 3 回たしざんするだけ。Excel で作ってみよう。
というわけで,図 2 ができたね。

でも,縦方向に見たときの数列は確かに図 1 と同じだけど,横方向に見ても図 1 には一致しないね。
よく回りを見回せば,図 1 の x = 11 の行は,図2の n=11,x^0 のマス目から右上へ黄色で色づけしたマス目の数値を読んでいけば得られる。すなわち,1, 10, 45, 112, 161, 126, 45, 4 だよ。
確率はだらだらと下がっていくようだけど,どんな風になるのかな。
この計算があっているかどうかも併せて,シミュレーションで確かめてみよう。ちょっと冗長なプログラムだけど,素直に書くと,
triple = function(p, k = 3) {
count = -3
while (TRUE) {
if ({count = count + 1; runif(1) < p}) {
if ({count = count + 1; runif(1) < p}) {
if ({count = count + 1; runif(1) < p}) {
return(count)
}
}
}
}
}
p = 0.3
x = replicate(1000000, triple(p))
plot(table(x))
median(x)
mean(x)

平均値は 48.54934,中央値は 33 ぐらいか。ずいぶん右裾が長いね。
計算結果ともよく合っていると思う。線が計算値,赤丸がシミュレーション値だよ。

x=12 のときと x=13 のときの確率が同じというのがちょっと気になるけど。
x Probability Simulated
0 0.02700000 0.026932
1 0.01890000 0.018876
2 0.01890000 0.018859
3 0.01890000 0.018700
4 0.01838970 0.018510
5 0.01803249 0.018055
6 0.01767528 0.017658
7 0.01731807 0.017579
8 0.01697050 0.017031
9 0.01662294 0.016504
10 0.01629563 0.016123
11 0.01596832 0.015904
12 0.01564757 0.015522
13 0.01564757 0.015265
14 0.01533327 0.014866
15 0.01502529 0.014577
16 0.01472348 0.014570
17 0.01442774 0.014255
18 0.01413795 0.013888
19 0.01385397 0.013625
20 0.01357569 0.013273
21 0.01330301 0.013093
これですっきりした。ありがとう。


















