よう!ヨッシーじゃないか。歩きながらポケモンやってると危ないよ。
おう!ジュンか。ついつい夢中になっちゃったんだけど,反省しないといけないね。
なんか,おもしろい話はないかい?
そうだねえ。ポケモンといえば,最近ポケモンの写真を何回か撮ると,何回目かに特別なポケモンが写真に写り込んでその特別なポケモンをゲットできるという機能が実装されたんだけど,1 回でゲットできることはほとんどなくて,大抵 2,30 回目にやっとゲットできるようなんだ。ゲットできるまでに何回くらい写真を撮らないといけないかは,1 回あたりのポケモンゲットの確率とどんな関係にあるんだろうね?
「確率 p で起きる事象が k 回起きるまでに,その事象が何回起きなかったか」という分布を負の二項分布というというのがあったね。
負の二項分布か〜。その分布は何で決まるの? p と k と...
それと,起きなかった回数 x だね。x はトライするたびに変わる。ヨッシーのいっているのは,k = 1 のときだけど,特別なポケモンが写真に写る確率 p は公表されていないよね。
起きなかった回数 x は,経験的に 20 〜 40 回くらいだと思うんだけど,平均的にはどれくらいなんだろうか。
さすがにオレも計算式は暗記していないし,これから講義があるから,それが終わってから昼休みの学食で続きをやろう。統計学の本を持って行くからヨッシーはノートパソコンを持ってこいよ。
じゃあ,後で...
:
さてと。負の二項分布は
f(x) = choose(x+k-1, x) * p^k * q^x
だね。
相変わらず,数式の表現は R の記法を拝借しているんだね(笑)でも,R なら関数が用意されているんじゃないか?
そう。dnbinom という関数がある。dnbinom(x, k, p) で そのときの確率 f(x) が得られる。
x は一つの値でなくて,ベクトルでも良いようだね。x = 0:30, k = 1。p はかなり低い気がするので,p = 0.1 でまずやってみよう。
> (prob = dnbinom(0:30, 1, 0.1))
[1] 0.100000000 0.090000000 0.081000000 0.072900000 0.065610000
[6] 0.059049000 0.053144100 0.047829690 0.043046721 0.038742049
[11] 0.034867844 0.031381060 0.028242954 0.025418658 0.022876792
[16] 0.020589113 0.018530202 0.016677182 0.015009464 0.013508517
[21] 0.012157665 0.010941899 0.009847709 0.008862938 0.007976644
[26] 0.007178980 0.006461082 0.005814974 0.005233476 0.004710129
[31] 0.004239116
それじゃよく分からないから,図にして。
じゃあ。
> plot(0:30, prob)

あれ!全然想像と違う。これじゃ,x = 0 のときが一番確率が高い。つまり 1 回目で事象が起きることがもっとも期待されるということだね。経験上は 2,30 回かかると思ってるんだけど。
平均値は k * (1-p) / p,分散は k * (1-p) / p^2 ということだ。平均値は 1.5,分散は 3.75 だ。
p が変わったらどうなるか,やってみよう。
> plot(0:30, dnbinom(0:30, 1, 0.2))
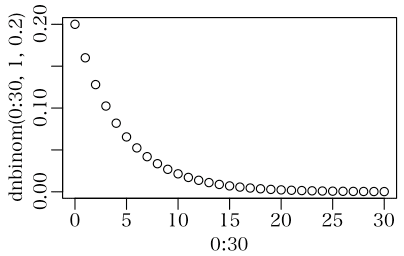
いろいろ変えても同じ傾向だね。x = 0 のときが一番確率が高い。
この分布の形って,k でも変わるよね。k = 5 ぐらいでやってみたら?
> plot(0:30, dnbinom(0:30, 5, 0.2))

あ。こんな感じ。も少し調整してみよう。
これでどうだい。
> plot(0:100, dnbinom(0:100, 8, 0.2))
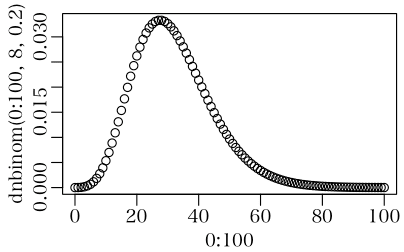
いい感じ。
平均値は 8 * 0.8 / 0.2 だから 32 だね。これは「事象が発生しなかった回数」だから,何回目に k 回事象が発生したかは 32+8 = 40 回目ということだね。
でも,どうやって解釈すればいいんだろうか?40 回目前後に当たりが出るようにでも設定しているのかなあ?
そうかもしれないけど,ゲームということを考えれば,1 ポイントとるごとにゲットされやすくなっていき,k ポイントとったらゲットできるようになっているのかもしれないね。そう考えれば,この問題は負の二項分布だけで説明できるんじゃないかな?
ポケモンもおもしろいけど,統計学もおもしろいね。
ハハハ。
=== おまけ ===
負の二項分布を R でシミュレーションしてみよう。
sim = function(k, p) {
count = -k # count は通算何回目に k 回目の事象が起こるかを表している
repeat {
count = count + 1
k = k - (runif(1) <= p) # 事象が発生したら k を 1 減らす
if (k == 0) { # 0 になったら結果を返す(事象が起きなかった回数)
return(count)
}
}
}
> k = 8
> p = 0.2
> q = 1-p
> z = replicate(10000, sim(k, p))
> mean(z) # シミュレーション結果の平均
[1] 31.9754
> k*q/p # 理論上の平均値
[1] 32
> var(z) # シミュレーション結果の分散
[1] 162.2052
> k*q/p^2 # 理論上の分散
[1] 160






















