データ処理の前処理って...

https://archive.ics.uci.edu/ml/datasets/water+treatment+plant
にある，water-treatment.data を読んで，データの様子を見る，というところまでやってみるというのを，
Julia だったらこうやるというところで...

using CSV, DataFrames

ヘッダーがないので，header=false を指定する。
欠損値は "?" ではいっているので，missingstring="?" とする。
日付データが dateformat="D-dd/mm/yy" の形で入っている（読み込んだ後は，年は 0090 とかになる。本当は 1990 年なんだろうけど），

df = CSV.read("water-treatment.data", DataFrame, header=false, missingstring="?", dateformat="D-dd/mm/yy");

先頭を見てみる。

first(df, 5)

5 rows × 39 columns (omitted printing of 30 columns)

Column1 Column2 Column3 Column4 Column5 Column6 Column7 Column8 Column9
Date… Int64? Float64? Float64 Int64? Int64? Int64? Float64? Float64?
1 0090-03-01 44101 1.5 7.8 missing 407 166 66.3 4.5
2 0090-03-02 39024 3.0 7.7 missing 443 214 69.2 6.5
3 0090-03-04 32229 5.0 7.6 missing 528 186 69.9 3.4
4 0090-03-05 35023 3.5 7.9 205 588 192 65.6 4.5
5 0090-03-06 36924 1.5 8.0 242 496 176 64.8 4.0

行数，列数を確認する。

size(df) # (527, 39)

第1列目（日付）でソートする（df は直接書き換えられるので，代入しなくてよい）。

sort!(df, :Column1)

527 rows × 39 columns (omitted printing of 30 columns)

先頭を見てみる。

first(df, 5)

Column1 Column2 Column3 Column4 Column5 Column6 Column7 Column8 Column9
Date… Int64? Float64? Float64 Int64? Int64? Int64? Float64? Float64?
1 0090-01-01 41230 0.35 7.6 120 344 136 54.4 4.5
2 0090-01-02 37386 1.4 7.9 165 470 170 76.5 4.0
3 0090-01-03 34535 1.0 7.8 232 518 220 65.5 5.5
4 0090-01-04 32527 3.0 7.8 187 460 180 67.8 5.2
5 0090-01-07 27760 1.2 7.6 199 466 186 74.2 4.5

using Plots

データが取られている日付の間隔をみるのだが，間隔は diff() だけで求まる。それをヒストグラムで表す。

histogram(diff(df[:, 1]))

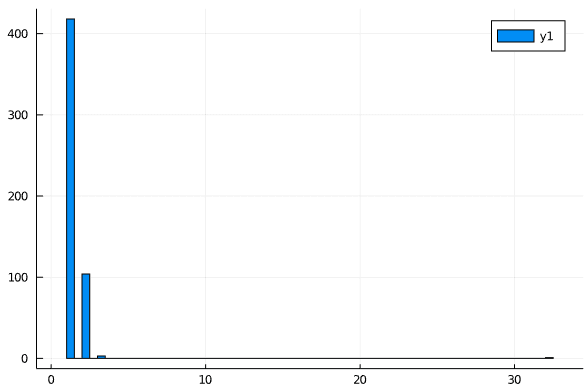
縦軸を対数表示にしたいということなので，yaxis=:log を指定する。

histogram(diff(df[:, 1]), yaxis=:log)

各項目（各列）で欠損値がどれくらいあるかということで，まずは，項目名と欠損値率を表示する。

hcat(names(df), describe(df)[:, :nmissing] ./ size(df,1))

39×2 Array{Any,2}:
 "Column1"   0.0
 "Column2"   0.0341556
 "Column3"   0.0056926
 "Column4"   0.0
 "Column5"   0.0436433
 ⋮           
 "Column38"  0.0151803
 "Column39"  0.0588235

棒グラフで見てもよいが。

bar(describe(df)[:, :nmissing] ./ size(df,1))

Julia のグラフで添え字などの表示

旨くいかないので，「.texで保存し、LaTeXでコンパイルしてpdfファイルを得ようとしている」という記事を読んで，やってみた。

一応できているのかな？

違うところは，Julia のバージョン？ Plots のバージョンは書いてなかったのでわからない。

using Plots

f(x) = sin(x)/x

g(x) = atan(x)

function plot_test()
    x = collect(-4:0.01:4) .* pi
    y1 = f.(x)
    y2 = g.(x)

    plot(x,y1,
        xaxis=(raw"$k_x$"),
        xlim=(-4pi, 4pi),
        xticks=(collect(-4:4) .* pi, ["$i \\pi" for i =-4:4]),
        yaxis=raw"$E_k$",
        label=raw"$f_k$",
        legend=:topleft,
        line=:solid
    )
    plot!(x,y2,
        label=raw"$\sigma_z$",
        legend=:topleft,
        line=:dash
    )

    annotate!(6, -0.8, Plots.text(raw"$\Sigma_\alpha=0.1 \textrm{eV/\AA}$", 16, :blue, :center))
end
plot_test()

3 次元空間の単位ベクトルを表す乱数（その4）

2014年8月5日に「3 次元空間の単位ベクトルを表す乱数」，2014年8月6日に「3 次元空間の単位ベクトルを表す乱数（その2）」という記事を2本書いた。

そのときは，ノルムが1より大きいベクトルを捨てていなかった。

n=3 のとき，ノルムが1より大きいベクトルを捨てないと，

のように，横軸が 1 〜2の間の頻度が比較的近い（横軸1あたりでカクンと変化がある）。

ノルムが1より大きいベクトルを捨ててシミュレーションすると，

のように，頭が丸くなる。

シミュレーションプログラムは以下の通り。

using Plots
plotly()

function sim(n=50000)
    xyz = (rand(n, 3) .- 0.5) .* 2
    r = vec(sum(xyz.^2, dims=2))
    xyz = xyz[r .<= 1, :]
    r = r[r .<= 1]
    factor = sqrt.(r)
    xyz ./ factor
end

function PearsonProblem(n = 4; dR = 0.1, trial = 100000)
    xyz = sim(2n*trial) # 歩留まり考慮の水増し発注
    N = size(xyz, 1)
    println(N÷n)
    dst = []
    for i = 1:n:N÷n
        dist = sqrt(sum(sum(xyz[i:i+n-1, :], dims=1) .^ 2))
        append!(dst, dist)
    end
    return dst
end

dst = PearsonProblem(3, trial=1000000);
histogram(dst)

 

球面上で一様に分布する点を表す x, y, z 座標値を生成する

「Julia でビュフォンの針」を書いたのには，速度比較だけではなく，もう一つ別の目的があったからなのだ。

ビュフォンの針のシミュレーションで，原点からのベクトルを考えるときに，方向がランダムなベクトルを作るときに，「長さが1以上のベクトルは除く」という操作をした後のベクトルだけを使わないと方向がランダムなベクトルは作れないということだった。

3次元空間でも同じで，球面に一様分布する点を表す座標を求めるときにも同じなのだ。-1 <= x, y, z <= 1 の一様乱数 x, y, z を発生させ，原点を起点，x, y, z を終点とするベクトルの内，ノルムが 1 より大きいは捨てる。ノルムが 1 以下のベクトルはノルムが 1 になるように伸ばすそうすれば，ベクトルの終点は球面に一様分布する。

以下のプログラムでできる x, y, z を，3次元空間にプロットできる。

グラフをぐりぐり動かすと点が一様分布している（らしい）ことが確認できる。

using Plots
plotly()

n=10000
xyz = (rand(n, 3) .- 0.5) .* 2
r = vec(sum(xyz.^2, dims=2))
xyz = xyz[r .<= 1, :] #@@@
r = r[r .<= 1] #@@@
factor = sqrt.(r)
xyz = xyz ./ factor
p = scatter(xyz[:, 1], xyz[:, 2], xyz[:, 3], markersize=0.1)

#@@@ を付けた 2 行を省いて，わかりやすくするために点の数を 5 倍にして図を描いてみると以下のようになる。濃淡があるということは，球面上で点が一様分布していないということである。

Julia でビュフォンの針

以前に掲載したが，π を使わないシミュレーション

n = 100000000 で，

Python 35.806 秒
R      14.543 秒
Julia   5.836 秒

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

★★　Python

import numpy as np
def buffon(n = 100000000): # 取りあえずの試行回数（実際はこれより少なくなる）
    d = 10 # 平行線の間隔
    l = d / 2 # 針の長さ
    # 以下 5 行で，0 <= theta < π/2 の一様乱数をもとめ，その sine.theta を生成する
    xy = np.random.rand(2, n) # 一辺 1 の正方形内の一様乱数による座標点
    r = (xy**2).sum(axis=0) # 原点からの距離
    xy = xy[:, r <= 1] # 半径 1 の円の内部にある点に限る
    r = r[r <= 1] # 半径 1 の円の内部にある点に限る
    sine_theta = xy[1,] / np.sqrt(r) # 三角関数の定義により
    n = len(r) # sine.theta の個数
    y = np.random.rand(n)*l # 同じ個数の[0, l) の一様乱数（針の中心から，平行線までの距離）
    return 2 * l / d / np.mean(y <= l / 2 * sine_theta) # 条件を満たすものの逆数が π の推定値

from time import time
s = time(); print(buffon(100000000), time() - s) # 3.1409810174102484 35.805713176727295

★★　R

buffon = function(n = 1e+06) { # 取りあえずの試行回数（実際はこれより少なくなる）
 d = 10 # 平行線の間隔
 l = d/2 # 針の長さ
 # 以下 5 行で，0 <= theta < π/2 の一様乱数をもとめ，その sine.theta を生成する
 xy = matrix(runif(2 * n, 0, 1), 2) # 一辺 1 の正方形内の一様乱数による座標点
 r = colSums(xy^2) # 原点からの距離
 xy = xy[, r <= 1] # 半径 1 の円の内部にある点に限る
 r = r[r <= 1] # 半径 1 の円の内部にある点に限る
 sine.theta = xy[2, ]/sqrt(r) # 三角関数の定義により
 n = length(r) # sine.theta の個数
 y = runif(n, 0, l) # 同じ個数の[0, l) の一様乱数（針の中心から，平行線までの距離）
 2 * l/d/mean(y <= l/2 * sine.theta) # 条件を満たすものの逆数が π の推定値
}

system.time(print(buffon(100000000)))
# [1] 3.141178
#    ユーザ   システム       経過  
#     14.543      2.852     17.349 

★★　Julia

function buffon(n = 1000000) # 取りあえずの試行回数（実際はこれより少なくなる）
    # 以下 5 行で，0 <= theta < π/2 の一様乱数をもとめ，その sinθ を生成する
    xy = rand(2, n);  # 一辺 1 の正方形内の一様乱数による座標点
    r = vec(sum(xy .^ 2, dims=1)); # 原点からの距離
    xy = xy[:, r .<= 1]; # 半径 1 の円の内部にある点に限る
    r = r[r .<= 1]; # 半径 1 の円の内部にある点に限る
    sinθ = xy[2, :] ./ sqrt.(r); # 三角関数の定義により
    n = length(r) # sinθ の個数
    n / sum(rand(n) .<= (0.5 .* sinθ)) # 条件を満たすものの逆数が π の推定値
end

@time buffon(100000000) #   5.836088 seconds (30 allocations: 7.269 GiB, 6.80% gc time)
# 3.141511691253939