using Polynomials
using Plots
gr(xlabel="\$x\$", ylabel="\$y\$", size=(400, 300))
多項式の定義,多項式の値,多項式の解
Polynomial() の目的は,1つには与えた係数ベクトルから「多項式 Polynomial{Float64, :x}」を作ることである。
係数ベクトルは定数項(0 次)から,1,2,3 次... の順に指定する。該当次数がないときは 0 を指定する。
p = Polynomial([1, 0, 3, 4]) # 1 + 3∙x^2 + 4∙x^3
typeof(p) # Polynomial{Float64, :x}
戻り値 p は関数でもあるので,plot() の第1引数(関数)としても使える。
plot(p, tick_direction=:out, title="\$1 + 3x^2 + 4x^3\$", label="")
hline!([0])
savefig("fig1.png")
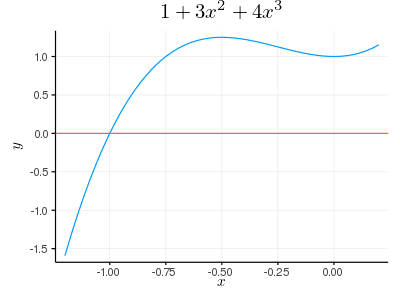
また,関数なので当然ながら,指定した値に対応する多項式の値を求めることもできる。
p(-1) # 0
p(-0.75) # 1.0
p(0) # 1
特に,多項式=0 の解を求めるには,roots() を使う。複素解も求まる。
roots(p)
#=
3-element Vector{ComplexF64}:
-1.0 + 0.0im
0.12500000000000006 - 0.4841229182759272im
0.12500000000000006 + 0.4841229182759272im
=#
多項式は,多項式 = 0 の解を a1, a2, ...としたとき,解のベクトル [a1, a2, ...] を指定して fromroots() で作成することもできる。
(x + 1.5) * (x - 2.2) * (x - 3.7) = 0 のとき,以下のように与える。
p = fromroots([-1.5, 2.2, 3.7]) # 12.21 - 0.7099999999999995∙x - 4.4∙x^2 + 1.0∙x^3
plot(p, tick_direction=:out, title="\$12.21 - 0.71^x - 4.4x^2 + 1.0 x^3\$", label="")
hline!([0])
savefig("fig2.png")
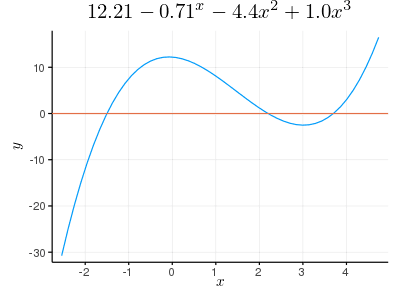
p(-1.5) # -3.552713678800501e-15
p(2.2) # -1.7763568394002505e-15
p(3.7) # 0.0
Machine.double.epsilon は eps() = 2.220446049250313e-16 なので,8eps()~16eps() 程度の誤差である。
eps() # 2.220446049250313e-16
8eps() # 1.7763568394002505e-15
16eps() # 3.552713678800501e-15
roots(p)
#=
3-element Vector{Float64}:
-1.4999999999999998
2.200000000000002
3.7
=#
p(-1.4999999999999998) # 1.7763568394002505e-15
p(2.200000000000002) # -1.2434497875801753e-14
p(3.7) # 0.0
多項式に用いる変数の指定
第二引数に「シンボル」で与えることができる(デフォルトは,前述の通り :x とするのと同じ)。
r = Polynomial([1,2,3], :a) # 1 + 2∙a + 3∙a^2
多項式の四則演算
四則演算の一部が使える。ただし,多項式に使われる変数が同じでなければならない。
p = Polynomial([1, 2]) # 1 + 2∙x
q = Polynomial([1, 0, -1]) # 1 - x^2
定数倍
2p # 2 + 4∙x
q/2 # 0.5 - 0.5∙x^2
定数和
3 + p # 4 + 2∙x
和
p +4q # 5 + 2∙x - 4∙x^2
差
p - q # 2∙x + x^2
積
p * q # 1 + 2∙x - x^2 - 2∙x^3
割り算
q ÷ p # 0.25 - 0.5∙x
div(q, p) # 0.25 - 0.5∙x
rem(q, p) # 0.75
divrem(q, p) # (Polynomial(0.25 - 0.5*x), Polynomial(0.75))
不定積分
y = Polynomial([1, 0, -1]) # 1 - x^2
z = integrate(y) # 1.0∙x - 0.3333333333333333∙x^3
微分
derivative(z) # 1.0 - 1.0∙x2 --> y に戻る
y = (x + 1) * (x - 2) * (x -4) の極値を求める。
多項式の定義
y = fromroots([-1, 2, 4])
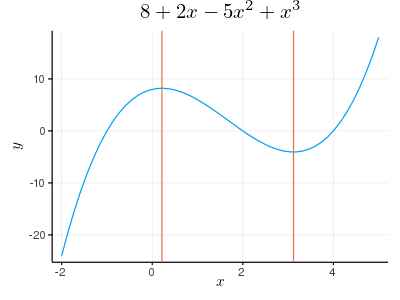
plot(y, tick_direction=:out, title="\$8 + 2x - 5x^2 + x^3\$", label="")
savefig("fig3.png")
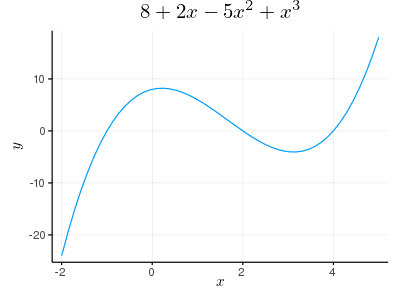
y の導関数を求めて(derivative),0 になるときの値 x を求める(roots)。
x = roots(derivative(y))
#=
2-element Vector{Float64}:
0.2137003521531088
3.1196329811802244
=#
vline!([x])
savefig("fig4.png")
多項式近似(多項式補間)
前報で述べたように,滑らかな単調増加・単調減少関数は多項式によって有効に近似できる。
正規分布の上側確率を求める近似式を作ってみる。
using Rmath
z値 に対する p 値の 9 対のデータに基づく。
z = 1:0.5:5 # z 値, 1.0:0.5:5.0
p = pnorm.(z, false) # p 値
#=
9-element Vector{Float64}:
0.15865525393145705
0.06680720126885807
0.022750131948179212
0.006209665325776135
0.0013498980316300946
0.00023262907903552494
3.1671241833119924e-5
3.39767312473006e-6
2.866515718791939e-7
=#
理論的に 8 次の近似式まで可能。
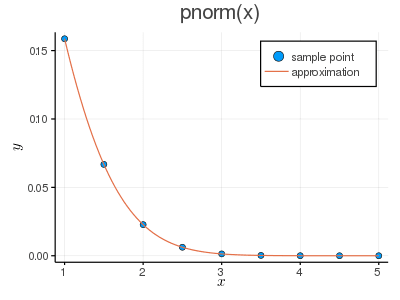
scatter(z, p, tick_direction=:out, title="pnorm(x)", label="sample point")
approx = fit(z, p); # length(z) - 1 次式(8 次式)で近似
見た目では差がわからないほどよく近似されているように見えるが。
plot!(approx, [1,5]..., label="approximation")
savefig("fig5.png")
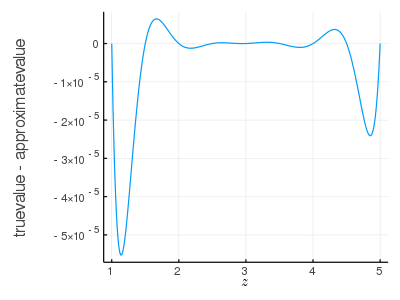
近似式を求めたのと同じ範囲の z をさらに細かく(0.01刻み)にして,真値と近似値の差をプロットしてみる。
z2 = collect(1:0.01:5);
truevalue = similar(z2);
approximatevalue = similar(z2);
for (i, z3) in enumerate(z2)
truevalue[i] = pnorm(z3, false)
approximatevalue[i] = approx(z3)
end
少なくとも小数点以下 4 桁程度まで正確であることがわかる。
plot(z2, (truevalue .- approximatevalue),
xlabel="\$z\$", ylabel="truevalue - approximatevalue", label="")
savefig("fig6.png")