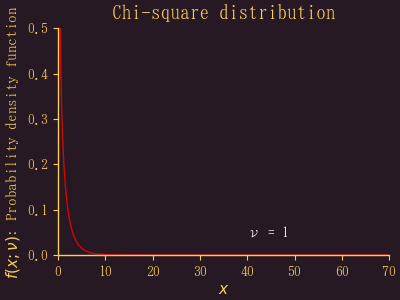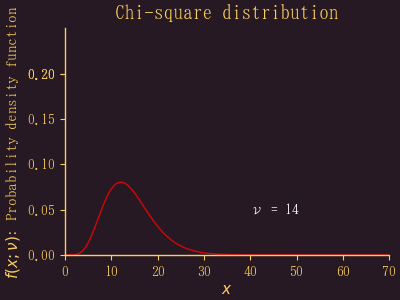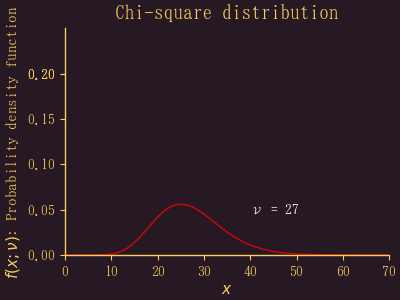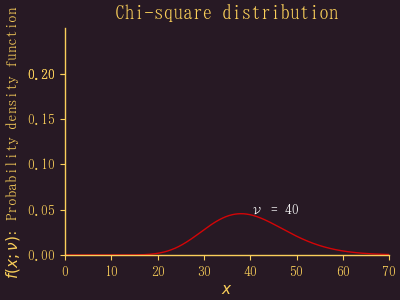
コイントスの結果は2項分布になるので,B(n, p-0.5) の n が大きくなれば正規分布に近づくというのは前に述べた。
コインの裏表を 1/0 で表して合計すると(平均値を求めても同じであるが)考えれば,一様分布に従う n 個のデータの和ということで,中心極限定理に従うことになると解釈できる。

サンプルプログラム
using Plots, PlotThemes, Random, Statistics, FreqTables
function centrallimittheorem2(nmax=20; fps=1)
Random.seed!(12345)
theme(:gruvbox_light)
pyplot(grid=false, label="", size=(400, 300))
n = 100000
anim = @animate for i = 1:nmax
data = vec(sum(reshape(rand(0:1, n*i), n, :), dims=2));
height = freqtable(data);
x = vec(names(height)...);
height = 100*vec(height) / n
bar(x, height, bar_width=1, linewidth=0,
xlims=(-0.5, nmax+0.5), ylimits=(0, 55),
tick_direction=:out, tickfontsize=10,
xlabel="表が出た枚数", ylabel="パーセント",
title="表が出た枚数の分布")
annotate!(10, 53,
text("$i 個のコインを投げるという試行を $n 回繰り返す", 8, :black))
end
gif(anim, "centralliittheorem2.gif", fps=fps)
end
centrallimittheorem2(20)