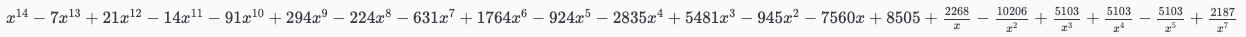1111111^2022を11111111で割った余りを求めよ。 ネタばらし注意

下へずっとスクロール

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Julia では長精度演算が簡単にできるので，一行で終了。

big(1111111)^2022 % 11111111

R だと 長精度演算 gmp ライブラリを使って

library(gmp)
as.bigz("1111111")^2022 %% 11111111

Python も gmpy を使って

import gmpy
gmpy.mpz(1111111)**2022 % 11111111

まあ，それでもあっという間に答えは出る。

この場合，長精度計算は不要なので，ライブラリを使わないでも以下で計算できる。
電卓ででもできる。まあ，2022回の掛算と剰余を求めるのは，大変だろうが。

x  = 1
for i = 1:2022
    x = (x * 1111111) % 11111111
end
println(x)

ここで，ちょっと途中結果を出力してみる。規則が見つかったので，i = 1:16 だけ計算する。

x  = 1
for i = 1:16
    x = (x * 1111111) % 11111111
    println("i = $i,  x = $x")
end
#=
i = 1,  x = 1111111
i = 2,  x = 1000000
i = 3,  x = 11011111
i = 4,  x = 10000
i = 5,  x = 11110111
i = 6,  x = 100
i = 7,  x = 11111101
i = 8,  x = 1
i = 9,  x = 1111111
i = 10,  x = 1000000
i = 11,  x = 11011111
i = 12,  x = 10000
i = 13,  x = 11110111
i = 14,  x = 100
i = 15,  x = 11111101
i = 16,  x = 1
=#
周期8で繰り返しています。
2022 % 8 = 6 なので，答えは xxx ですね。

ところで，Python や Julia には引数を 3 つ持つ pow, powermod がある。

pow(1111111, 2022, 11111111)
powermod(1111111, 2022, 11111111)

で答えが出る。

この場合も，長精度計算は不要。

R の gymp にも同じ計算をする関数 powm がある。
powm(1111111, 2022, 11111111)

 

数学問題をSymPyで解く

(x^2 - x +3/x)^7 を展開したときの，x^9 の係数はいくつか？

解説が書いてあるが，読む暇があったら，以下を打ち込む。

using SymPy
@syms x
expand((x^2 - x +3/x)^7)

答え一発，

 

大学入試などで，このような問題が出し続けられるのはいかがなものか？

数学的考え方を醸成する？

醸成したら何が起きる？