数学検定 過去問題 準1級（高校3年程度） 問題1. 不等式を解く
https://www.su-gaku.net/suken/support/past_questions/
〔準１級〕１次：計算技能検定
問題1. 次の不等式を解きなさい。
using SymPy
@syms x
eq1 = log(1/2, 2x)
eq2 = log(1/2, x^2-2x+3)
solve(Eq(eq1, eq2)) # [1, 3]
以下はエラーになる。
solve(Ge(eq1, eq2))
図を描いて確定する。
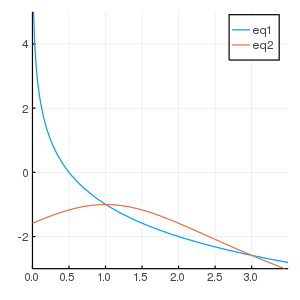
using Plots
plot(eq1, xlims=(0.0, 3.5), ylims=(-3, 5), size=(300, 300), label="eq1")
plot!(eq2, label="eq2")
0 < x < 1, 3 < x
数学検定 過去問題
https://www.su-gaku.net/suken/support/past_questions/
1級（大学程度・一般）
〔１級〕１次：計算技能検定
問題7. xyz空間における領域 V={ (x，y，z) | ０≦x≦y≦z≦１} に対して，次の３重積分を求
めなさい。
紙と鉛筆でやるとなると，めんどくさいんだろうなあ。
using SymPy
@syms x y z
integrate(x^3 * y^2 * z, (x, 0, y), (y, 0, z), (z, 0, 1)) # 1/252
数学検定 過去問題
https://www.su-gaku.net/suken/support/past_questions/
1級（大学程度・一般）
〔１級〕１次：計算技能検定
問題6. 次の行列の固有値を求めなさい。
[ 3 -1 2
-2 5 -3
1 -3 2 ]
定石通り，以下の固有方程式を解く。
using SymPy
@syms λ
M = [ 3-λ -1 2
-2 5-λ -3
1 -3 2-λ]
ev = det(M) # -λ^3 + 10*λ^2 - 18*λ + 4
solve(ev) # 2, 4 - sqrt(14), sqrt(14) + 4
別解というか，こちらの方がよい
M = [ 3 -1 2
-2 5 -3
1 -3 2 ]
#=
3×3 Matrix{Int64}:
3 -1 2
-2 5 -3
1 -3 2
=#
sympy.Matrix(M).eigenvals()
#=
Dict{Any, Any} with 3 entries:
4 - sqrt(14) => 1
sqrt(14) + 4 => 1
2 => 1
=#
数学検定 過去問題
https://www.su-gaku.net/suken/support/past_questions/
1級（大学程度・一般）
〔１級〕１次：計算技能検定
問題5. 0 以上の整数値をとる確率変数 X が下の確率分布に従うとき，次の問いに答えなさい。
ただし binomial(n, r) は二項係数を表します。
P(X=k) = binomial(k+2, k) * (1/10)^2 * (9/10)^k * (1/10)
(1) X の期待値 E(X) を求めなさい。
(2) X の分散 V(X) を求めなさい。
これは，数値解なので Julia プログラムを書いても求まる（ただし，途中までの部分和）
e = 0
for k = 0:4000
p = binomial(k+2, k) * (1/10)^2 * (9/10)^ k * (1/10)
e += k*p
end
println(e) # 27.000000000000046 期待値
v = 0
for k = 0:4000
p = binomial(k+2, k) * (1/10)^2 * (9/10)^ k * (1/10)
v += (k-s)^2*p
end
println(v) # 270.00000000000006 分散
SymPy では summation() を使う。
using SymPy
@syms k
p = binomial(k+2, k) * (1/10)^2 * (9/10)^ k * (1/10)
mean = summation(k * p, (k, 0, oo)) # 27.0
variance = summation((k-mean)^2 * p, (k, 0, oo)) # 270.0
数学検定 過去問題
https://www.su-gaku.net/suken/support/past_questions/
1級（大学程度・一般）
〔１級〕１次：計算技能検定
問題4. 関数f(x)＝x^2 * e^(－x) について，次の問いに答えなさい。ただし，eは自然対数の底を表しま
す。
① f(x) の第5次導関数の x=-1 における値f^{(5)}(-1) を求めなさい。
② f(x) の第10次導関数の x=-1 における値f^{(10)}(-1) を求めなさい。
using SymPy
@syms x
f = x^2 * ℯ^(-x) # x^2*exp(-x)
diff(f, x, 5).subs(x, -1) # -31*E ie. -31ℯ
diff(f, x, 10).subs(x, -1) # 111*E ie. 111ℯ
ちなみに，
diff(f, x, 5) |> string # "(-x^2 + 10*x - 20)*exp(-x)"
diff(f, x, 10) |> string # "(x^2 - 20*x + 90)*exp(-x)"
数学検定 過去問題
https://www.su-gaku.net/suken/support/past_questions/
1級（大学程度・一般）
〔１級〕１次：計算技能検定
問題3. xyz 空間における 2 平面 3x−y−2z＝6, x + 2y - 3z = 4 が交わってできる直線を l とします。l を含み，点(1, -1, -2) を通る平面の方程式を求めなさい。
using SymPy
@syms x, y, z, k
2 平面の方程式を a, b とおく。
a = 3x - y - 2z - 6 # = 0
b = x + 2y - 3z - 4 # = 0
求める平面の方程式は a + k * b = 0 とおける。
eq1 = a + k * b
# k*(x + 2*y - 3*z - 4) + 3*x - y - 2*z - 6
この平面が (x, y, z) = (1, -1, -2) を通るので，x, y, z に代入し，eq1 = 0 を k について解く。
solve(eq1.subs([(x, 1), (y, -1), (z, -2)]), k)
k = -2 である。
eq1 に k = -2 を代入して解を得る。
eq1.subs(k, -2)
# x - 5*y + 4*z + 2
数学検定 過去問題
https://www.su-gaku.net/suken/support/past_questions/
1級（大学程度・一般）
〔１級〕１次：計算技能検定
問題2. 次の値を求めなさい。ただし，sin(z) ，cos(z) はそれぞれ複素数 z に関する正弦関数，余弦関数で，i は虚数単位を表します。
cos(６i) －i sin(６i)
単純にやると結果が数値で出てしまう。
using SymPy
simplify(cos(6im)-complex(0,1)*sin(6im)) # 403.4287934927351 - 0.0im
対数をとってみると
log(cos(6im)-im*sin(6im)) # 6.0 - 0.0im ==> 6
なので
ℯ^6 # 403.4287934927351
であることがわかる。
しかし，これは結果論だな。
Julia の SymPy では，変数の型を指定できる。a, b を複素数として，
@syms a::complex b::complex
simplify(simplify(cos(a) - b * sin(a)).subs(b, im)) # 1.0*exp(-I*a)
となる。
a = 6im
なので
-im * a # 6 + 0im
よって，1.0ℯ^-ia == ℯ^6
ただし，これも結果がわかっているときに試行錯誤的に解を求めていることに違いはない。
たとえば，
simplify(cos(a) - b * sin(a)).subs(a, 6im)
では
-201.713157370279*I*b + 201.715636122456
になってしまう。
