算額(その56)
宮城県角田市横倉 愛宕神社 明治15年(1882)1月
http://www.wasan.jp/miyagi/yokokuraatago.html
外円の中に大小 8 個の円が入っている。それぞれの径を求めよ。
外円の半径を 1 として,図のように記号を定め,方程式を解く。

using SymPy
@syms or1::positive, ir1::positive
@syms or2::positive, ir2::positive
@syms or3::positive, oy3::positive, ir3::positive, ix3::positive, iy3::positive
eq1 = or3^2 + (oy3 - ir1)^2 - (ir1 + or3)^2;
eq2 = ix3^2 + (iy3 - or1)^2 - (or1 + ir3)^2;
eq3 = or3^2 + (2 - ir2 - oy3)^2 - (ir2 + or3)^2;
eq4 = ix3^2 + (2 - or2 - iy3)^2 - (or2 + ir3)^2;
eq5 = or3^2 + (oy3 - 1)^2 - (1 - or3)^2;
eq6 = ix3^2 + (iy3 - 1)^2 - (1 - ir3)^2;
eq7 = or1 + or2 - 1;
eq8 = (oy3 - 1)/or3 - (iy3 - 1)/ix3;
eq9 = (ix3 - or3)^2 + (iy3 - oy3)^2 - (or3 - ir3)^2;
方程式が複雑になるとどうも solve() では解けないこともでてくるようだ。
そこで,nlsolve() を使うことにする。
# solve([eq1, eq2, eq3, eq4, eq5, eq6, eq7, eq8, eq9])
eq1 |> expand |> println
eq2 |> expand |> println
eq3 |> expand |> println
eq4 |> expand |> println
eq5 |> expand |> println
eq6 |> expand |> println
eq7 |> expand |> println
eq8 |> expand |> println
eq9 |> expand |> println
-2*ir1*or3 - 2*ir1*oy3 + oy3^2
-ir3^2 - 2*ir3*or1 + ix3^2 + iy3^2 - 2*iy3*or1
-2*ir2*or3 + 2*ir2*oy3 - 4*ir2 + oy3^2 - 4*oy3 + 4
-ir3^2 - 2*ir3*or2 + ix3^2 + iy3^2 + 2*iy3*or2 - 4*iy3 - 4*or2 + 4
2*or3 + oy3^2 - 2*oy3
-ir3^2 + 2*ir3 + ix3^2 + iy3^2 - 2*iy3
or1 + or2 - 1
oy3/or3 - 1/or3 - iy3/ix3 + 1/ix3
-ir3^2 + 2*ir3*or3 + ix3^2 - 2*ix3*or3 + iy3^2 - 2*iy3*oy3 + oy3^2
using NLsolve
function nls(func, params...; ini = [0.0])
if typeof(ini) <: Number
r = nlsolve((vout, vin) -> vout[1] = func(vin[1], params...), [ini], ftol=1e-14)
v = r.zero[1]
else
r = nlsolve((vout, vin)->vout .= func(vin, params...), ini, ftol=1e-14)
v = r.zero
end
return v, r.f_converged
end;
function h(u)
or1, ir1, or2, ir2, or3, oy3, ir3, ix3, iy3 = u
return [
-2*ir1*or3 - 2*ir1*oy3 + oy3^2,
-ir3^2 - 2*ir3*or1 + ix3^2 + iy3^2 - 2*iy3*or1,
-2*ir2*or3 + 2*ir2*oy3 - 4*ir2 + oy3^2 - 4*oy3 + 4,
-ir3^2 - 2*ir3*or2 + ix3^2 + iy3^2 + 2*iy3*or2 - 4*iy3 - 4*or2 + 4,
2*or3 + oy3^2 - 2*oy3,
-ir3^2 + 2*ir3 + ix3^2 + iy3^2 - 2*iy3,
or1 + or2 - 1,
oy3/or3 - 1/or3 - iy3/ix3 + 1/ix3,
-ir3^2 + 2*ir3*or3 + ix3^2 - 2*ix3*or3 + iy3^2 - 2*iy3*oy3 + oy3^2
];
end;
iniv = [89, 8, 49, 27, 58, 185, 40, 75, 200] ./ 135;
res = nls(h, ini=iniv)
names =["or1", "ir1", "or2", "ir2", "or3", "oy3", "ir3", "ix3", "iy3"]
println(res[2])
for (name, value) in zip(names, res[1])
println("$name = $value")
end
true
or1 = 0.7023666314613604
ir1 = 0.5412673937726713
or2 = 0.2976333685386396
ir2 = 0.17483505787654022
or3 = 0.41809549294196335
oy3 = 1.4047332629227232
ir3 = 0.2642988189720262
ix3 = 0.5285976379440508
iy3 = 1.5117037863118916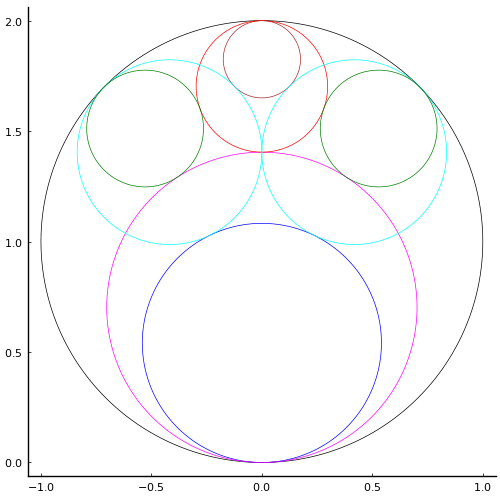
using Plots
function circle(ox, oy, r, color=:red; beginangle=0, endangle=360)
θ = beginangle:0.1:endangle
x = r.*cosd.(θ)
y = r.*sind.(θ)
plot!(ox .+ x, oy .+ y, color=color, linewidth=0.5)
end;
function point(x, y, string="", color=:green, position=:left, vertical=:top; mark=true)
mark && scatter!([x], [y], color=color, markerstrokewidth=0)
annotate!(x, y, text(string, 10, position, color, vertical))
end;
function draw(more=false; fill=false)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
plot()
or1 = 0.7023666314613604
ir1 = 0.5412673937726713
or2 = 0.2976333685386396
ir2 = 0.17483505787654022
or3 = 0.41809549294196335
oy3 = 1.4047332629227232
ir3 = 0.2642988189720262
ix3 = 0.5285976379440508
iy3 = 1.5117037863118916
circle(0, 1, 1, :black)
circle(0, ir1, ir1, :blue)
circle(0, or1, or1, :magenta)
circle(0, 2-ir2, ir2, :brown)
circle(0, 2-or2, or2, :red)
circle(or3, oy3, or3, :cyan)
circle(ix3, iy3, ir3, :green)
circle(-or3, oy3, or3, :cyan)
circle(-ix3, iy3, ir3, :green)
if more
point(0, 1, " 1", :black)
point(0, ir1, " ir1", :blue)
point(0, or1, " or1", :magenta)
point(0, 2-ir2, " 2-ir2", :brown)
point(0, 2-or2, " 2-or2", :red)
point(or3, oy3, "(or3,oy3)", :cyan)
point(ix3, iy3, "(ix3,iy3),ir3", :green, :center)
vline!([0], color=:black, lw=0.5)
hline!([0], color=:black, lw=0.5)
end
end;


















