算額（その69）

算額（その69）

長野県長野市篠井 長谷観音堂 亨和3年(1803)
http://www.wasan.jp/nagano/hasekannon.html

直角三角形の中に大円と小円が斜線で区切られて入っている。大円，小円の径がそれぞれ 32 尺，24 尺である。 

鉤，股，弦を求めよ。

注：直角三角形の直角を挟む短い辺（鉤）と長い辺（股）と直角に対する辺（弦）

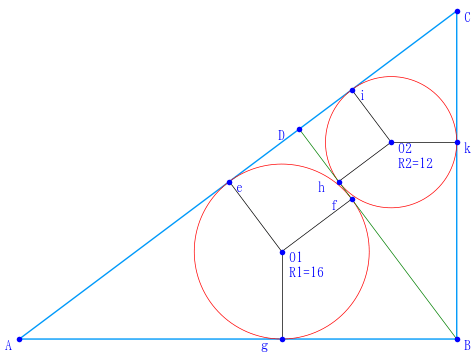
図のように記号を定め，方程式を解く。

using SymPy
@syms AB::positive, BC::positive, BD::positive, AD::positive, CD::positive;

各線分が整数になるように BD=12 と仮置して割合を求める。

eq1 = BD^2 + AD^2 - AB^2;
eq2 = BD^2 + CD^2 - BC^2;
eq3 = 16BC - 12AB;
eq4 = 16BD - 12AD;
eq5 = BD - 12;

solve([eq1, eq2, eq3, eq4, eq5], (AB, BC, BD, AD, CD))

   1-element Vector{NTuple{5, Sym}}:
    (20, 15, 12, 16, 9)

三角形 ABD において，AB, BD, AD の長さは実際は 20n, 12n, 16n (n は整数) であり，その中に半径 16 の円が内接している。

Ag = Ae, Bg = Bf, De = Df = 16

Ag + Bg = AB = 20n

Ae + De = Ae + 16 = AD = 16n より，Ae = 16n - 16 = Ag

Bf + Df = Bf + 16 = BD = 12n より，Bf = 12n - 16 = Bg

Ag + Bg = 28n - 32 = AB = 20n より，8n = 32 で，n = 4

すなわち，AB, BD, AD の長さは実際は 20n=80, 12n=48, 16n=64

三角形 ABD とBCD は相似比 4:3 なので BC = 80*3/4 = 60, CD = 48*3/4 = 36

以上から，直角三角形の直角を挟む短い辺（鉤）の長さは BC = 60, 長い辺（股）の長さは AB = 80，直角に対する辺（弦）の長さは AD + CD = 64 + 36 = 100 であることがわかる。

using Plots

function circle(ox, oy, r, color=:red; beginangle=0, endangle=360)
   θ = beginangle:0.1:endangle
   x = r.*cosd.(θ)
   y = r.*sind.(θ)
   plot!(ox .+ x, oy .+ y, color=color, linewidth=0.5)
end;

function point(x, y, string="", color=:green, position=:left, vertical=:top; mark=true)
   mark && scatter!([x], [y], color=color, markerstrokewidth=0)
   annotate!(x, y, text(string, 10, position, color, vertical))
end;

function segment(x1, y1, x2, y2, color=:black; linestyle=:solid, linewidth=0.5)
   plot!([x1, x2], [y1, y2], color=color, linestyle=linestyle, linewidth=linewidth)
end

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   plot([0, 80, 80, 0], [0, 0, 60, 0], xlims=(-5, 85), ylims=(-5, 65))
   circle(48, 16, 16)
   circle(80 - 12, 36, 12)
   x3, y3 = 48 .* [0.6, 0.8]
   segment(80, 0, 80 - x3, y3, :green)
   if more
       plot!(showaxis=false)
       x1, y1 = 48 .* [0.8, 0.6]
       segment(48, 16, x1, y1)
       segment(48, 16, 48, 0)
       x2, y2 = 32 .* [0.6, 0.8]
       segment(48, 16, 80 - x2, y2)
       x4, y4 = 12 .* [0.8, 0.6]
       segment(80 - 12, 36, 80, 36)
       segment(80 - 12, 36, 80 - 12 - x4, 36 - y4)
       x5, y5 = 12 .* [0.6, 0.8]
       segment(80 - 12, 36, 80 - 12 - x5, 36 + y5)
       point(x1, y1, " e", :blue)
       point(80-x2, y2, "f  ", :blue, :right)
       point(48, 0, "g  ", :blue, :right)
       point(80-x3, y3, "D  ", :blue, :right)
       point(80 - 12 - x4, 36 - y4, "h  ", :blue, :right)
       point(80 - 12 - x5, 36 + y5, " i", :blue)
       point(80, 36, " k", :blue)
       point(0, 0, "A ", :blue, :right)
       point(80, 0, " B", :blue)
       point(80, 60, " C", :blue)
       point(48, 16, " O1\n R1=16", :blue)
       point(80-12, 36, " O2\n R2=12", :blue)
   end
end;

算額（その68）

算額（その68）

新潟県柏崎市 椎谷観音堂 寛政7年(1795)5月
http://www.wasan.jp/niigata/shiiyahukugen.png

外円の中に、弦と外円に接する甲円 1 個，乙円 2 個がある。外円の径が 5 寸であるとき，弦と甲円の径の差が最も大きくなるような乙円の径を求めよ。

答えは 1 寸

外円の半径を 5 とし，図のように記号を定め，方程式を解く。

弦（の 1/2）と r2 の差は以下である。

using SymPy
@syms r2::positive
gen = sqrt((5^2 - (5 - 2r2)^2)) - r2
gen |> println

   -r2 + sqrt(25 - (5 - 2*r2)^2)

これが最も大きくなるのは gen の導関数が 0 になるときの r2 である。

r2 = solve(diff(gen))[1]
println("r2 = $r2 = $(r2.evalf())")

   r2 = 5/2 - sqrt(5)/2 = 1.38196601125011

using Plots
plot(gen, color=:black, aspectratio=:none, ylims=(0, 3.5), size=(500, 300), label="")
xlabel!("y2")
ylabel!("gen")
vline!([r2], label="")

r2 = 5/2 - sqrt(5)/2 として，二本の方程式を立て，解く。

@syms x1, r1
r2 = 5//2 - sqrt(Sym(5))/2
eq1 = x1^2 +(5 - 2r2 + r1)^2 - (5 - r1)^2;
eq2 = x1^2 + (r2 - r1)^2 - (r2 + r1)^2;

solve([eq1, eq2], (x1, r1))

   2-element Vector{Tuple{Sym, Sym}}:
    (-sqrt(10 - 2*sqrt(5)), 1)
    (sqrt(10 - 2*sqrt(5)), 1)

2 組目の解が適切な解である。すなわち，乙円の径は 1 である。
また，乙円の中心座標は，（sqrt(10 - 2*sqrt(5)), 1+sqrt(5)) である。

using Plots

function circle(ox, oy, r, color=:red; beginangle=0, endangle=360)
   θ = beginangle:0.1:endangle
   x = r.*cosd.(θ)
   y = r.*sind.(θ)
   plot!(ox .+ x, oy .+ y, color=color, linewidth=0.5)
end;

function point(x, y, string="", color=:green, position=:left, vertical=:top; mark=true)
   mark && scatter!([x], [y], color=color, markerstrokewidth=0)
   annotate!(x, y, text(string, 10, position, color, vertical))
end;

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   plot(ylims=(-0.2, 5.1))
   r2 = 5/2 - sqrt(5)/2
   x1, r1 = (sqrt(10 - 2*sqrt(5)), 1)
   gen = sqrt(5^2 - (5 - 2r2)^2)
   println("x1 = $x1;  r1 = $r1;  r2 = $r2")
   println("弦 = $gen;  差 = $(gen - r2)")
   circle(0, 0, 5)
   circle(0, 5-r2, r2, :blue)
   circle(x1, 5-2r2+r1, r1, :magenta)
   hline!([5-2r2])
   if more
       point(0, 5-r2, "5-r2 ", :blue, :right)
       point(0, 5-2r2, "5-2r2 ", :blue, :right)
       point(x1, r1+√5, "(x1,r1+√5))", :blue, :center)
       hline!([0], color=:black, lw=0.5)
       vline!([0], color=:black, lw=0.5)
   end
end;

   x1 = 2.3511410091698925;  r1 = 1;  r2 = 1.381966011250105
   弦 = 4.47213595499958;  差 = 3.0901699437494745