Julia / v1.9.1 での新機能の二つ目

今まで，ユニコード文字列のスライスに手こずっていたけど，Unicode.graphemes() でなんとかうまくいくようになった。多バイト文字とASCIIなどが混じっていても文字単位でスライスできる。

In [23]: a = "私の名前は中野です"

Out[23]: "私の名前は中野です"

In [24]: a[2:5]  # これはエラーになる

ERROR: StringIndexError: invalid index [2], valid nearby indices [1]=>'私', [4]=>'の'

Stacktrace:

[1] string_index_err(s::String, i::Int64)

   @ Base ./strings/string.jl:12

[2] getindex(s::String, r::UnitRange{Int64})

   @ Base ./strings/string.jl:277

[3] top-level scope

   @ REPL[24]:1

[4] top-level scope

   @ /Applications/Julia-1.9.app/Contents/Resources/julia/share/julia/stdlib/v1.9/REPL/src/REPL.jl:1416

In [25]: using Unicode  # こうやっておいて

In [26]: graphemes(a, 3:7)  # こうすれば，うまくいく

Out[26]: "名前は中野"

Julia / v1.9.1 での新機能の一つ

新しい機能で，入力と出力に番号プレフィックスをつけることができるようになった。

しかし，println() を使うとその機能が使えない。バグ？

julia> using REPL  # まずはこれをやらないといけないのかな?

julia> REPL.numbered_prompt!()  # ついで，これ。

In [2]: (a, b) = (2, 45)

Out[2]: (2, 45)

In [3]: println(a + 2b)  # println() の出力には[番号]がつかない

92

In [4]: a + 2b  # REPL だと，つく。

Out[4]: 92

Julia / Current stable release: v1.9.1 (June 7, 2023)

Julia が v1.9.1 へバージョンアップされました

Current stable release: v1.9.1 (June 7, 2023)

算額（その273）

算額（その273）

中村信弥「改訂増補 長野県の算額」
http://www.wasan.jp/zoho/zoho.html
県内の算額（165）
長野県飯山市下木島 鳥出神社 天保14年(1843)

大円内に中円 1 個，小円 2 個が入っている。外円，中円の径を知って小円の径を求めよ。

大円の半径と中心座標を R, (0, 0) とする。
中円の半径と中心座標を r1, (0, R - r1) とする。
右下の小円の半径と中心座標を r2, (r2, y2) とする。

以下の連立方程式を解く。

include("julia-source.txt");

using SymPy
@syms R::positive, r1::positive, r2::positive, y2::negative;

eq1 = r2^2 + y2^2 - (R - r2)^2
eq2 = r2^2 + (R - r1 - y2)^2 - (r1 + r2)^2
res = solve([eq1, eq2], (r2, y2))

   1-element Vector{Tuple{Sym, Sym}}:
    ((-R + r1)*(-R + (R^2 - 3*R*r1)/(R + r1))/(R + r1), (R^2 - 3*R*r1)/(R + r1))

res[1][1] |> simplify |> println  # r2: 小円の半径
res[1][2] |> simplify |> println  # y2: 小円の中心の y 座標

   4*R*r1*(R - r1)/(R + r1)^2
   R*(R - 3*r1)/(R + r1)

R = 140寸, r1 = 84寸 のとき，小円の半径 r2 = 52寸5分である。直径は 105 寸である。

(R, r1) = (140, 84)
4*R*r1*(R - r1)/(R + r1)^2

   52.5

using Plots

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (R, r1) = (140, 84)
   r2 = 4*R*r1*(R - r1)/(R + r1)^2
   y2 = R*(R - 3*r1)/(R + r1)
   @printf("r2 = %.6f;  y2 = %.6f\n", r2, y2)
   plot()
   circle(0, 0, R, :black)
   circle(0, R - r1, r1, :blue)
   circle(r2, y2, r2)
   circle(-r2, y2, r2)
   if more
       point(R, 0, " R", :black, :left, :bottom)
       point(0.7R, R - 1.7r1, "大円:R\n(0,0)", :black, mark=false)
       point(0, R - r1, " 中円:r1\n (0,R-r1)", :blue)
       point(r2, y2, " 小円:r2\n (r2,y2)", :red)
       vline!([0], color=:black, lw=0.5)
       hline!([0], color=:black, lw=0.5)
   else
       plot!(showaxis=false)
   end
end;

算額（その272）

算額（その272）

中村信弥「改訂増補 長野県の算額」
http://www.wasan.jp/zoho/zoho.html
県内の算額（257）
長野県下高井郡野沢温泉村 湯沢神社 明治17年(1884)

円内に等円 3 個，三角形 1 個が入っている。等円の径を知って三角形の高さを求めよ。

右下の等円の半径と中心座標を r, (r, R - 3r) とする。
外円の半径を R とすると，三角形の頂点 A の座標(x0, y0) で，y0 = R - 2r, x0 = sqrt(R^2 - (R - 2r)^2) である。
上の等円の中心から線分 AB への距離が r である。
以下の連立方程式を解く。

include("julia-source.txt");

using SymPy
@syms R::positive, r::positive, x::positive, y::negative, x0::positive, y0::positive, x1::positive, y1::positive;

y0 = R - 2r
x0 = sqrt(R^2 - (R - 2r)^2)
eq2 = x1^2 + y1^2 - R^2
eq3 = distance(x0, y0, x1, y1, 0, R - r) - r^2
eq4 = r^2 + (R - 3r)^2 - (R - r)^2;

res = solve([eq2, eq3, eq4], (R, x1, y1))

   1-element Vector{Tuple{Sym, Sym, Sym}}:
    (9*r/4, 2*sqrt(5)*r/9, 79*r/36)

   R = 2.250000;  x1 = 0.496904;  y1 = 2.194444;  y0 = 0.250000
   三角形の高さ: y1 - y0 = (35/18)*r = 1.944444

y1 - y0 が三角形の高さなので，79r/36 - (9r/4 - 2r) = (35/18)*r である。

using Plots

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   r = 1
   R = 9r/4
   y0 = R - 2r
   x0 = sqrt(R^2 - (R - 2r)^2)
   (R, x1, y1) = (9*r/4, 2*sqrt(5)*r/9, 79*r/36)
   @printf("R = %.6f;  x1 = %.6f;  y1 = %.6f;  y0 = %.6f\n", R, x1, y1, y0)
   @printf("三角形の高さ: y1 - y0 = (35/18)*r = %.6f\n", (35/18)*r)
   plot()
   circle(0, 0, R, :black)
   circle(r, R - 3r, r)
   circle(-r, R - 3r, r)
   circle(0, R - r, r)
   plot!([x0, x1, -x0, x0], [y0, y1, y0,  y0], color=:blue, lw=0.5)
   if more
       point(x1, y1, " B:(x1,y1)", :black, :left, :bottom)
       point(x0, y0, "A:(x0,y0)  ", :black, :right, :bottom)
       point(0, R, " R", :black, :left, :bottom)
       point(r, R - 3r, "(r,R-3r)", :red)
       point(0, R - r, " R-r", :red)
       vline!([0], color=:black, lw=0.5)
       hline!([0], color=:black, lw=0.5)
   else
       plot!(showaxis=false)
   end
end;

 

算額（その271）

算額（その271）

中村信弥「改訂増補 長野県の算額」
http://www.wasan.jp/zoho/zoho.html
県内の算額（256）
長野県下高井郡野沢温泉村 湯沢神社 明治17年(1884)

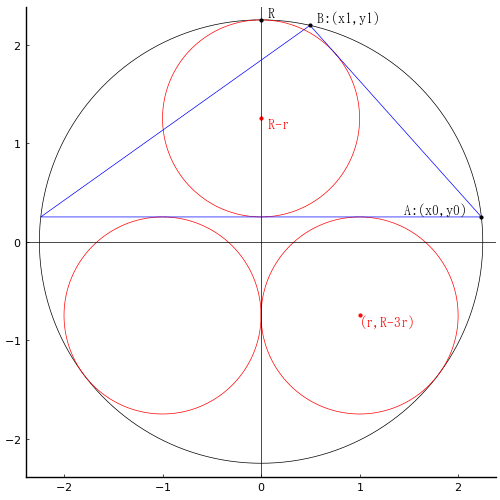
直線の上に天円 2 個が互いに外接している。月円 4 個も直線に外接し両端の月園は天円にも外接している。人円 2 個は月円 2 個と，天円および日円に外接している。日円は天円とも外接している。天円の径を知って月円の径を求めよ。

y 軸が天円の交点を通るようにして，右半分だけを考える。
天円の半径，中心座標を r1, (r1, r1)
日円の半径，中心座標を r2, (0, y2)
人円の半径，中心座標を r3, (x3, y3)
月円の半径，中心座標を r4, (r4, r4) および (3r4, r4)

天円と右端の月円が外接することから，天円の径が与えられれば月円の径は方程式 1 本で解ける。

include("julia-source.txt");

using SymPy
@syms r1::positive, r2::positive, r3::positive, r4::positive, y2::positive, x3::positive, y3::positive;

r1 = 1
eq3 = (r1 -3r4)^2 + (r1 - r4)^2 - (r1 + r4)^2 |> expand
solve(eq3, r4) |> println

   Sym[r1/9, r1]

r4 < r1 なので r4 = r1 / 9，すなわち月円の径は天円の径の 1/9 である。

以下の連立方程式を解いて残りのパラメータを求める。

@syms r1::positive, r2::positive, r3::positive, r4::positive, y2::positive, x3::positive, y3::positive;

r1 = 1
r4 = r1//9
eq1 = r1^2 + (r1 - y2)^2 - (r1 + r2)^2 |> expand
eq2 = (r1 - x3)^2 + (r1 - y3)^2 - (r1 + r3)^2 |> expand
eq4 = x3^2 + (y2 - y3)^2 - (r2 + r3)^2 |> expand
eq5 = (x3 - 3r4)^2 + (y3 - r4)^2 - (r3 + r4)^2 |> expand
eq6 = r4^2 + (y2 - r4)^2 - (r2 + r4)^2 |> expand;

res = solve([eq1, eq2, eq4, eq5, eq6], (r2, y2, r3, x3, y3))

   1-element Vector{NTuple{5, Sym}}:
    (8*r1/45, 17*r1/45, 2*r1/27, 2*r1/9, 7*r1/27)

日円の径は天円の径の 8/45，人円の径は天円の径の 2/27 などである。

using Plots

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   r1 = 1
   r4 = r1/9
   (r2, y2, r3, x3, y3) = (8*r1/45, 17*r1/45, 2*r1/27, 2*r1/9, 7*r1/27)
   @printf("月円: r4 = %.6f\n", r4)
   plot()
   circle(r1, r1, r1)
   circle(-r1, r1, r1)
   circle(0, y2, r2, :blue)
   circle(x3, y3, r3, :magenta)
   circle(-x3, y3, r3, :magenta)
   circle(r4, r4, r4, :green)
   circle(3r4, r4, r4, :green)
   circle(-r4, r4, r4, :green)
   circle(-3r4, r4, r4, :green)
   if more
       point(r1, r1, " 天円:r1,(r1,r1)", :red)
       point(0, y2, " 日円:r2,(0,r2)", :blue, :left, :bottom)
       point(x3, y3, " 人円:r3,(x3,y3)", :magenta, :left, :bottom)
       point(r4, r4, " 月円:r4,(r4,r4)", :green, :left, :bottom)
       point(3r4, r4, " 月円:r4,(3r4,r4)", :green, :left, :top)
       vline!([0], color=:black, lw=0.5)
       hline!([0], color=:black, lw=0.5, xlims=(-0.1, 2), ylims=(-0.05, 1.1))
   else
       plot!(showaxis=false)
       hline!([0], color=:black, lw=0.5)
   end
end;