算額(その1418)
百五十三 多野郡新町 諏訪神社 年代不明
群馬県和算研究会:群馬の算額,上武印刷株式会社,高崎市,1987年3月31日.
キーワード:球,体積,定積分
#Julia, #SymPy, #算額, #和算
直径が 80 寸の玉がある。水平に切断し,8 等分に分割する。それぞれの厚み(甲矢,乙矢,丙矢,丁矢)はいかほどか。
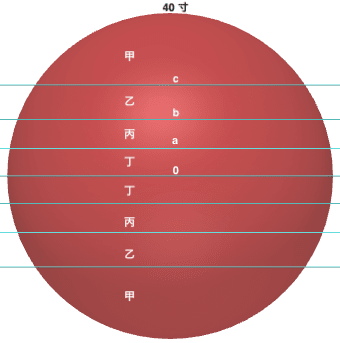
切断位置の z 座標を a, b, c とする。
甲矢 = 40 - c
乙矢 = c - b
丙矢 = b - a
丁矢 = a
である。
以下の連立方程式を解く。27組の解が得られるが 14 番目のものが適解である。
とはいっても,形式上は虚数解であるが,虚数部が実質 0 なので,実数部をとればよい。
include("julia-source.txt");
# julia-source.txt ソース https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf
using SymPy
@syms R, x, a, b, c
#R = 80/2
eq1 = integrate((R^2 - x^2)*PI, (x, c, R)) - PI*R^3*4/3 / 8
eq2 = integrate((R^2 - x^2)*PI, (x, b, c)) - PI*R^3*4/3 / 8
eq3 = integrate((R^2 - x^2)*PI, (x, a, b)) - PI*R^3*4/3 / 8
eq4 = integrate((R^2 - x^2)*PI, (x, 0, a)) - PI*R^3*4/3 / 8
res = solve([eq1, eq2, eq3], (a, b, c))[14] # 14 of 27
(-3*R^2/((-1/2 - sqrt(3)*I/2)*(27*R^3/4 + 27*sqrt(15)*sqrt(-R^6)/4)^(1/3)) - (-1/2 - sqrt(3)*I/2)*(27*R^3/4 + 27*sqrt(15)*sqrt(-R^6)/4)^(1/3)/3, -3*R^2/((-1/2 - sqrt(3)*I/2)*(27*R^3/2 + 27*sqrt(3)*sqrt(-R^6)/2)^(1/3)) - (-1/2 - sqrt(3)*I/2)*(27*R^3/2 + 27*sqrt(3)*sqrt(-R^6)/2)^(1/3)/3, -3*R^2/((-1/2 - sqrt(3)*I/2)*(81*R^3/4 + 27*sqrt(7)*sqrt(-R^6)/4)^(1/3)) - (-1/2 - sqrt(3)*I/2)*(81*R^3/4 + 27*sqrt(7)*sqrt(-R^6)/4)^(1/3)/3)
甲矢 = 17.685; 乙矢 = 8.42313; 丙矢 = 7.16168; 丁矢 = 6.73018 である。
a = res[1](R => 40).evalf() |> real
b = res[2](R => 40).evalf() |> real
c = res[3](R => 40).evalf() |> real
(a, b, c) |> println
(6.73017607124110, 13.8918542133544, 22.3149879332610)
@printf("甲矢 = %g; 乙矢 = %g; 丙矢 = %g; 丁矢 = %g\n", 40 - c, c - b, b- a, a)
甲矢 = 17.685; 乙矢 = 8.42313; 丙矢 = 7.16168; 丁矢 = 6.73018



























