算額（その447）

算額（その447）

河□狭山牛頭天王社 林助右衛門自弘 寛政7年乙卯11月(1795) 

藤田貞資(1789)：神壁算法巻上
http://www.wasan.jp/jinpeki/jinpekisanpo1.pdf

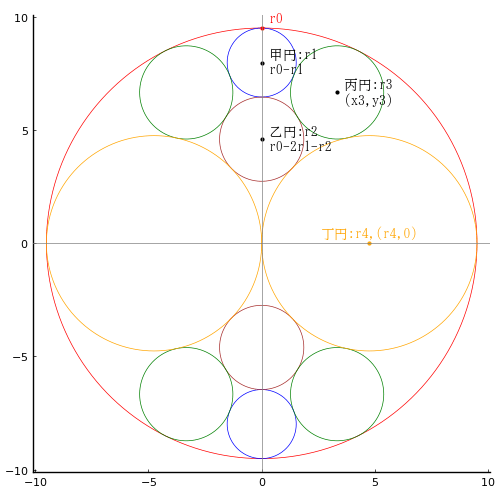
図のように 12 個の円がある。甲円，乙円，丙円の直径がそれぞれ 43寸7分5厘，51寸0分3厘，141寸7分5厘のとき丁円の直径はいかほどか。

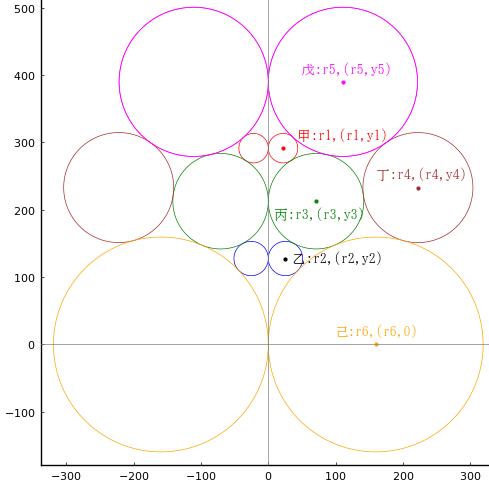
左右対称なので，右半分の図形で方程式を立てる。
甲円の半径と中心座標を r1, (r1, y1)
乙円の半径と中心座標を r2, (r2, y2)
丙円の半径と中心座標を r3, (r3, y3)
丁円の半径と中心座標を r4, (x4, y4)
戊円の半径と中心座標を r5, (r5, y5)
己円の半径と中心座標を r6, (r6, 0)
とおき，連立方程式の解を求める。

include("julia-source.txt")

using SymPy

@syms r1::positive, y1::positive,
     r2::positive, y2::positive,
     r3::positive, y3::positive,
     r4::positive, x4::positive, y4::positive,
     r5::positive, y5::positive,
     r6::positive;

(r1, r2, r3) = (4375, 5103, 14175) .// 200
eq1 = (r1 - r3)^2 + (y1 - y3)^2 - (r1 + r3)^2
eq2 = (r1 - r5)^2 + (y1 - y5)^2 - (r1 + r5)^2
eq3 = (r2 - r3)^2 + (y2 - y3)^2 - (r2 + r3)^2
eq4 = (r6 - r2)^2 + y2^2 - (r2 + r6)^2
eq5 = (r3 - r5)^2 + (y3 - y5)^2 - (r3 + r5)^2
eq6 = (r3 - r6)^2 + y3^2 - (r3 + r6)^2
eq7 = (x4 - r5)^2 + (y4 - y5)^2 - (r4 + r5)^2
eq8 = (r3 - x4)^2 + (y3 - y4)^2 - (r3 + r4)^2
eq9 = (x4 - r6)^2 + y4^2 - (r4 + r6)^2;
res = solve([eq1, eq2, eq3, eq4, eq5, eq6, eq7, eq8, eq9], (y1, y2, y3, r4, x4, y4, r5, y5, r6))

   3-element Vector{NTuple{9, Sym}}:
    (1071/8, 5103/40, 1701/8, 189/920, 84861/920, 26649/184, 14175/128, 567/16, 5103/32)
    (1071/8, 5103/40, 1701/8, 6048/215, 18333/860, 43659/344, 2025/224, 162, 5103/32)
    (2331/8, 5103/40, 1701/8, 3267/40, 8883/40, 1863/8, 14175/128, 6237/16, 5103/32)

3 組目のものが適解である。

   r1 = 21.875;  r2 = 25.515;  r3 = 70.875
   y1 = 291.375;  y2 = 127.575;  y3 = 212.625;  r4 = 81.675;  x4 = 222.075;  y4 = 232.875;  r5 = 110.742;  y5 = 389.812;  y6 = 159.469

丁円の直径は 2*3267/40 = 163.35, 163寸3分5厘である。

2*3267/40

   163.35

using Plots

function circle2(x, y, r, color)
   circle(x, y, r, color)
   circle(-x, y, r, color)
end

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (r1, r2, r3) = (4375, 5103, 14175) .// 200
   (y1, y2, y3, r4, x4, y4, r5, y5, r6) = [305, 138, 224, 85, 225, 252, 106.0, 403, 174.4]
   (y1, y2, y3, r4, x4, y4, r5, y5, r6) = res[3]
   @printf("r1 = %g;  r2 = %g;  r3 = %g\n", r1, r2, r3)
   @printf("y1 = %g;  y2 = %g;  y3 = %g;  r4 = %g;  x4 = %g;  y4 = %g;  r5 = %g;  y5 = %g;  y6 = %g\n", y1, y2, y3, r4, x4, y4, r5, y5, r6)
   @printf("丁円の直径 = %g\n", 2r4)
   plot()
   circle2(r1, y1, r1, :red)
   circle2(r2, y2, r2, :blue)
   circle2(r3, y3, r3, :green)
   circle2(x4, y4, r4, :brown)
   circle2(r5, y5, r5, :magenta)
   circle2(r5, y5, r5, :magenta)
   circle2(r6, 0, r6, :orange)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /  3  # size[2] * fontsize * 2
       point(r1, y1, "  甲:r1,(r1,y1)", :red, :left, :bottom, delta=delta)
       point(r2, y2, " 乙:r2,(r2,y2)", :black, :left, :vcenter)
       point(r3, y3, " 丙:r3,(r3,y3)", :green, :center, :top, delta=-delta)
       point(x4, y4, " 丁:r4,(r4,y4)", :brown, :center, :bottom, delta=delta)
       point(r5, y5, " 戊:r5,(r5,y5)", :magenta, :center, :bottom, delta=delta)
       point(r6,  0, "己:r6,(r6,0)", :orange, :center, :bottom, delta=delta)
       hline!([0], color=:gray, lw=0.5)
       vline!([0], color=:gray, lw=0.5)
   else
      plot!(showaxis=false)
   end
end;

算額（その446）

算額（その446）

寛政7年乙卯10月(1795) 久留米 鈴木半平正晟
藤田貞資(1807)：続神壁算法
http://www.wasan.jp/jinpeki/zokujinpekisanpo.pdf

外円内に甲，乙，丙，丁の 4 種類の円が入っている。それぞれ隣り合う円に外接し，外円に内接している。甲円の直径が 3寸0分5厘のとき，外円の直径はいかほどか。

外円の半径と中心座標を r0, (0, 0)
甲円の半径と中心座標を r1, (0, r0 - r1)
乙円の半径と中心座標を r2, (0, r0 - 2r1 - r2, 0)
丙円の半径と中心座標を r3, (x3, y3)
丁円の半径と中心座標を r4, (r4, 0)
とおき，連立方程式の解を求める。

include("julia-source.txt")

using SymPy

@syms r0::positive, r1::positive,
     r2::positive, r3::positive, x3::positive, y3::positive,
     r4::positive;

r1 = 305//200
r4 = r0//2
eq1 = x3^2 + (r0 - r1 - y3)^2 - (r1 + r3)^2
eq2 = x3^2 + (y3 - r0 +2r1 + r2)^2 - (r2 + r3)^2
eq3 = r4^2 + (r0 - 2r1 - r2)^2 - (r2 + r4)^2
eq4 = (x3 - r4)^2 + y3^2 - (r3 + r4)^2
eq5 = x3^2 + y3^2 - (r0 - r3)^2;
# res = solve([eq1, eq2, eq3, eq4, eq5], (r0, r2, r3, x3, y3));

using NLsolve

function nls(func, params...; ini = [0.0])
   if typeof(ini) <: Number
       r = nlsolve((vout, vin) -> vout[1] = func(vin[1], params..., [ini]), ftol=big"1e-40")
       v = r.zero[1]
   else
       r = nlsolve((vout, vin)->vout .= func(vin, params...), ini, ftol=big"1e-40")
       v = r.zero
   end
   return v, r.f_converged
end;

function H(u)
   (r0, r2, r3, x3, y3) = u
   return [
       x3^2 - (r3 + 61/40)^2 + (r0 - y3 - 61/40)^2,  # eq1
       x3^2 - (r2 + r3)^2 + (-r0 + r2 + y3 + 61/20)^2,  # eq2
       r0^2/4 - (r0/2 + r2)^2 + (r0 - r2 - 61/20)^2,  # eq3
       y3^2 + (-r0/2 + x3)^2 - (r0/2 + r3)^2,  # eq4
       x3^2 + y3^2 - (r0 - r3)^2,  # eq5
   ]
end;

r1 = 305//200
iniv = [big"10.0", 2, 2, 2, 7]
res = nls(H, ini=iniv);
names = ("r0", "r2", "r3", "x3", "y3")
if res[2]
   for (name, x) in zip(names, res[1])
       @printf("%s = %g;  ", name, round(Float64(x), digits=6))
   end
   println()
else
   println("収束していない")
end;

   r0 = 9.51;  r2 = 1.86053;  r3 = 2.05932;  x3 = 3.33205;  y3 = 6.66409;  

外円の直径は 2r0 = 19.02 つまり，19寸0分2厘。

using Plots

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   r1 = 305//200
   (r0, r2, r3, x3, y3) = [24.0, 5, 5, 9, 17]
   (r0, r2, r3, x3, y3) = res[1]
   r4 = r0/2
   @printf("r0 = %g;  r1 = %g;  r2 = %g;  r3 = %g;  x3 = %g;  y3 = %g\n", r0, r1, r2, r3, x3, y3)
   @printf("外円の直径 = %g\n", 2r0)
   plot()
   circle(0, 0, r0, :red)
   circle(0, r0 - r1, r1, :blue)
   circle(0, r1 - r0, r1, :blue)
   circle(0, r0 - 2r1 - r2, r2, :brown)
   circle(0, 2r1 + r2 - r0, r2, :brown)
   circle4(x3, y3, r3, :green)
   circle(r4, 0, r4, :orange)
   circle(-r4, 0, r4, :orange)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /  3  # size[2] * fontsize * 2
       point(0, r0 - r1, " 甲円:r1\n r0-r1", :black, :left, :vcenter)
       point(0, r0 - 2r1 - r2, " 乙円:r2\n r0-2r1-r2", :black, :left, :vcenter)
       point(x3, y3, " 丙円:r3\n (x3,y3)", :black, :left, :vcenter)
       point(r4, 0, "丁円:r4,(r4,0)", :orange, :center, :bottom, delta=delta/2)
       point(0, r0, " r0", :red, :left, :bottom, delta=delta/2)
       hline!([0], color=:gray, lw=0.5)
       vline!([0], color=:gray, lw=0.5)
   else
      plot!(showaxis=false)
   end
end;

Juliaを使用してJupyter Labでリポータブルなデータ分析を行う方法

Juliaを使用してJupyter Labでリポータブルなデータ分析を行う方法

リポータブルなデータ分析は，データの分析，結果の文書化，そして他の人と共有するための効果的な方法である。Juliaプログラミング言語とJupyter Labを組み合わせて，リポータブルなデータ分析を行う方法について紹介する。

Jupyter Labとは何か？

Jupyter Labは，インタラクティブなコンピューティング環境を提供するオープンソースのプロジェクトである。データ分析，機械学習，プロトタイピングなどのさまざまなタスクに適している。Julia言語を含む多くのプログラミング言語と統合でき，コード，テキスト，図表などを組み合わせた文書を作成できる。

リポータブルなデータ分析のステップ

1. Jupyter Labのインストールとセットアップ

まず，Jupyter Labをインストールし，JuliaをJupyter Labで使用できるようにセットアップする。JuliaのREPL（Read-Eval-Print Loop）で次のコマンドを実行する。

using Pkg
Pkg.add("IJulia")

これにより，JuliaのカーネルがJupyter Labで利用可能になる。

2. 新しいJupyterノートブックの作成

Jupyter Labを起動し，新しいノートブックを作成する。Juliaのカーネルを選択して，コードセルを実行する準備が整う。

3. データの読み込みと前処理

データ分析の最初のステップは，データを読み込み，必要な前処理を行うことである。Juliaのパッケージを使用してデータを読み込み，データのクリーニング，欠損値の処理，データの変換などを行う。

using CSV
data = CSV.File("data.csv") |> DataFrame
# データの前処理

4. データの可視化

Plots.jlやStatsPlots.jlを使用して，データの可視化を行う。プロットを作成し，データの特性やパターンを視覚的に理解しよう。

5. 分析と結果の文書化

Jupyterノートブックは，コードセルとテキストセルを組み合わせた文書を作成できる。コードセルで分析を行い，テキストセルで結果を説明し，洞察を提供する。Markdown形式を使用してテキストを書き込むことができる。

6. グラフや表の挿入

リポータブルなデータ分析において，結果を明確に伝えるために図表を挿入する。Plots.jlで作成したプロットをノートブックに埋め込み，データのビジュアルな表現を提供する。

# プロットを表示
plot(data, x=:x, y=:y, label="データ")

7. ノートブックのエクスポート

データ分析が完了したら，JupyterノートブックをHTML，PDF，または他のフォーマットにエクスポートして他の人と共有できる。

結論

JuliaとJupyter Labを組み合わせて，リポータブルなデータ分析を行うことは容易である。データの読み込み，可視化，分析，文書化，そして共有のステップを追いながら，洞察に富んだデータ分析レポートを作成できる。このプロセスは，データ駆動の意思決定をサポートし，プロジェクトやビジネスの成功に貢献する。