算額(その861)改訂版
算額(その861)は,そもそも問と図が一致していないので,改訂版を書く。
参考文献
1). 二十四 岩手県一関萩荘 達古袋八幡神社 弘化3年(1846)
山村善夫:現存 岩手の算額,昭和52年1月30日,熊谷印刷,盛岡市.
http://www.wasan.jp/yamamura/yamamura.html
2). 今有如図 03030
https://w.atwiki.jp/sangaku/pages/289.html
キーワード:円3個,円弧,正三角形2個
#Julia, #SymPy, #算額, #和算
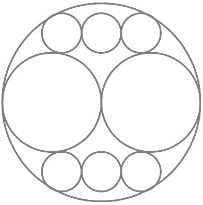
円弧(弓形)の中に,正三角形 2 個,小円 2 個,大円 1 個を容れる。正三角形の一辺の長さ,小円の直径が与えられたとき,大円の直径を求める術を述べよ。
山村は「小円 2 個,大円 1 個を容れる」と言っているのに,中央に小円 1 個のみ描いている。

筆者も,問題文をよく確認せずに誤った解釈で「算額(その861)」を書いてしまった。痛恨の極みである。
「今有如図」ではちゃんと,小円 2 個,大円 1 個 が描かれている。

よって,「算額(その861)改訂版」を書くことになった。

しかしなお,この場合も,「正三角形の一辺の長さと,任意の小円の直径の両方が与えられた場合には図を描くことができない」ことに変わりはない。そこで,「正三角形の一辺の長さのみが与えられる」ものとして解を求めることにする。
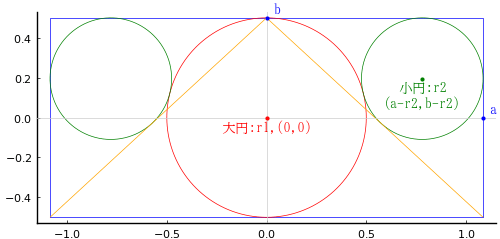
正三角形の一辺の長さを a
円弧の半径と中心座標を R, (0, 0)
大円の半径と中心座標を r1, (0, R - r1)
小円の半径と中心座標を r2, (x2, R - 2r1 + r2)
とおき,a を既知として以下の連立方程式を解き (R, r1, r2, x2) を求める。
条件式が 4 個あるのだから,未知数は 4 個でなければならない。a, r2 が与えられてしまうと条件式が余る。使われない条件式を満たさない解になるということである。(今更こんなことを書く必要はないのだが)
include("julia-source.txt");
# julia-source.txt ソース https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf
using SymPy
@syms R, a, r1, r2, x2
y = R - 2r1
b = y/sqrt(Sym(3))
eq1 = dist(b, y, b + a/2, y + sqrt(Sym(3))*a/2, 0, R - r1) - r1^2
eq2 = dist(b + a, y, b + a/2, y + sqrt(Sym(3))*a/2, x2, y + r2) - r2^2
eq1 = dist2(b, y, b + a/2, y + sqrt(Sym(3))*a/2, 0, R - r1, r1)
eq2 = dist2(b + a, y, b + a/2, y + sqrt(Sym(3))*a/2, x2, y + r2, r2)
eq3 = x2^2 + (y + r2)^2 - (R - r2)^2
eq4 = (b + a/2)^2 + (y + sqrt(Sym(3))*a/2)^2 - R^2;
#res = solve([eq1, eq3, eq4], (R, r1, r2, x2))
res = solve([eq1, eq4], (R, r1))[4] # 4 of 4
((-669*sqrt(3)*a^3*(-24*sqrt(3)/23 - 16/23)^2/32 + 81*sqrt(3)*a^3*(-24*sqrt(3)/23 - 16/23)/8 + 18*sqrt(3)*a^3 - 5313*sqrt(3)*a^3*(-24*sqrt(3)/23 - 16/23)^3/512)/(26*a^2), -sqrt(3)*a*(-24*sqrt(3)/23 - 16/23)/8)
# R
res[1] |> simplify |> println
3*a*(2*sqrt(3) + 9)/23
円弧の直径は,正三角形の一辺の長さの 6(2√3 + 9)/23 倍である。
# r1
res[2] |> simplify |> println
a*(2*sqrt(3) + 9)/23
大円の直径は,正三角形の一辺の長さの 2(2√3 + 9)/23 倍である。
大円の直径は,正三角形の一辺の長さのみで決定される。そして,このあと判明するが,小円の直径も正三角形の一辺の長さのみで決定される。小円の直径として任意の値を設定すると,そのような図形は描けないということになる。
引き続き,eq2, eq3 から x2, r2 を求める。
eq12 = eq2(R => res[1], r1 => res[2]) |> simplify;
# x2
ans_x2 = solve(eq12, x2)[2] |> factor # of 2
ans_x2 |> println
(9*sqrt(3)*a + 75*a + 23*sqrt(3)*r2)/69
eq13 = eq3(R => res[1], r1 => res[2], x2 => ans_x2) |> simplify;
# r2
ans_r2 = solve(eq13, r2)[1] |> sympy.sqrtdenest |> factor # of 2
ans_r2 |> println
a*(-27 + 17*sqrt(3))/23
小円の直径は正三角形の一辺の長さの 2(17√3 - 27)/23 倍である。
なお,a を r2 で表すこともできるので,r2 を与えて r1 を求めることもできる。それは,他のパラメータと r1 の関係にも成り立つ。
eq = r2 - a*(-27 + 17*sqrt(Sym(3)))/23;
ans_a = solve(eq, a)[1] |> factor
ans_a |> println
r2*(27 + 17*sqrt(3))/6
以前求めた r1 の式中に出てくる a に ans_a を代入すれば,r2 から r1 を求める式になる。
ans_r1 = res[2](a => ans_a) |> simplify
ans_r1 |> println
r2*(5 + 3*sqrt(3))/2
ans_r1(r2 => 0.212596845971384).evalf() |> println
1.08383492305546
いずれにせよ,r1 を求めるためには,a か r2 のいずれかだけがわかればよいということである。
以上をまとめると,正三角形の一辺の長さが 1 のとき,大円,小円,円弧の直径は 1.08383492305546, 0.212596845971384, 3.25150476916637 である。
a = 1
R = 3*a*(2*sqrt(3) + 9)/23
r1 = a*(2*sqrt(3) + 9)/23
r2 = a*(-27 + 17*sqrt(3))/23
2 .*(r1, r2, R)
(1.083834923055457, 0.21259684597138379, 3.2515047691663708)
術は「大円直径 = (√12*正三角形の一辺の長さ - 小円直径)/3」ということで,r2 に 0.1062984229856919 以外の値が与えられると成り立たない。
a = 1
r2 = 0.1062984229856919
(√12*a - 2r2)/3 |> println
1.083834923055457
function draw(a, more=false)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
R = 3*a*(2√3 + 9)/23
r1 = a*(2√3 + 9)/23
r2 = a*(17√3 - 27)/23
x2 = (9√3*a + 75*a + 23√3*r2)/69
@printf("正三角形の一辺の長さが %g のとき,大円,小円,円弧の直径は %.15g, %.15g, %.15g である。\n", a, 2r1, 2r2, 2R)
@printf("a = %g; R = %g; r1 = %g; r2 = %g; x2 = %g\n", a, R, r1, r2, x2)
b = (R - 2r1)/√3
y = R - 2r1
x = sqrt(R^2 - y^2)
θ = atand(y, x)
plot([b, b + a, b + a/2, b], [y, y, y + √3a/2, y], color=:blue, lw=0.5)
plot!(-[b, b + a, b + a/2, b], [y, y, y + √3a/2, y], color=:blue, lw=0.5)
circle(0, 0, R, :magenta, beginangle=θ, endangle=180 - θ)
circle(0, R - r1, r1)
circle2(x2, y + r2, r2, :green)
segment(-x , y, x, y)
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
hline!([0], color=:gray80, lw=0.5)
vline!([0], color=:gray80, lw=0.5)
ylims!(y - 10delta, R + 3delta)
point(b + a, y, "(b+a,y)", :blue, :center, delta=-delta/2)
#point(b + a/2, y, "(b+a/2,y)", :blue, :center, delta=-delta/2)
point(b + a/2, y + √3a/2, "(b+a/2,y+√3a/2)", :blue, :center, :bottom, delta=5delta, deltax=15delta)
point(b, y, "(b,y)", :blue, :center, delta=-delta/2)
point(0, y, "(0,y)", :blue, :center, delta=-delta/2)
point(0, y + r1, "大円:r1,(0, y+r1)", :red, :center, delta=-delta/2)
point(x2, y + r2, "小円:r2\n(x2, y+r2)", :green, :right, :vcenter, delta=delta, deltax=-13delta)
point(0, R, "R", :magenta, :center, :bottom, delta=delta)
point(b + a/2, y + √3a/2)
end
end;
draw(1, true)