算額(その1494)
参考文献
1). 二 岩手県花巻市大田 音羽山清水観世音堂 明治25年(1892)
山村善夫:現存 岩手の算額,昭和52年1月30日,熊谷印刷,盛岡市.
http://www.wasan.jp/yamamura/yamamura.html
2). 今有如図 03076
https://w.atwiki.jp/sangaku/pages/137.html
キーワード:円5個,外円,直角三角形2個
#Julia, #SymPy, #算額, #和算
外円内に交差する直角三角形を 2 個容れ,隙間に大円 1 個,中円 2 個,小円 1 個を容れる。小円の直径が与えられたとき,外円の直径を求める術を述べよ。
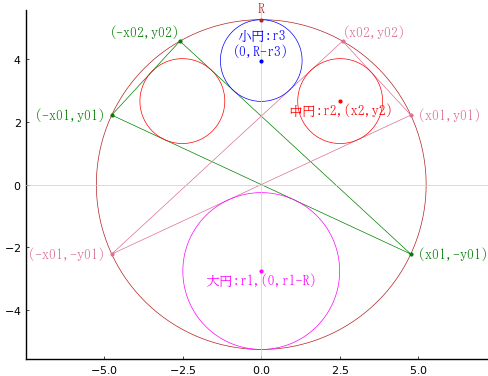
注:直角三角形の斜辺は外円の直径である(外円の中心を通る)。
外円の半径と中心座標を R, (0, 0)
大円の半径と中心座標を r1, (0, r1 - R)
中円の半径と中心座標を r2, (x2, y2)
小円の半径と中心座標を r3, (0, R - r3)
直角三角形の円周上にある頂点の座標を (x01, y01), (-x01, -y01), (x02, y02)
とおき,以下の連立方程式を解き (R, r1, r2, x2, y2, x01, x02) を求める。
include("julia-source.txt");
# julia-source.txt ソース https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf
using SymPy
@syms R, r1, r2, x2, y2, r3, x01, y01, x02, y02
# y01 = sqrt(R^2 - x01^2)
# y02 = sqrt(R^2 - x02^2)
eq1 = dist2(-x01, -y01, x02, y02, 0, R - r3, r3)
eq2 = dist2(-x01, -y01, x02, y02, x2, y2, r2)
eq3 = dist2(-x01, -y01, x01, y01, x2, y2, r2)
eq4 = dist2(-x01, -y01, x01, y01, 0, r1 - R, r1)
eq5 = dist2(x01, y01, x02, y02, x2, y2, r2)
eq6 = (x01 - x02)^2 + (y02 - y01)^2 + (x02 + x01)^2 + (y02 + y01)^2 - 4R^2
eq7 = sqrt((x01 - x02)^2 + (y02 - y01)^2) + sqrt((x02 + x01)^2 + (y02 + y01)^2) - 2R - 2r2;
# res = solve([eq1, eq2, eq3, eq4, eq5, eq6, eq7], (R, r1, r2, x2, y2, x01, x02))
function H(u)
(R, r1, r2, x2, y2, x01, x02) = u
y01 = sqrt(R^2 - x01^2)
y02 = sqrt(R^2 - x02^2)
return [
R^2*x01^2 + 2*R^2*x01*x02 + R^2*x02^2 - 2*R*r3*x01^2 - 4*R*r3*x01*x02 - 2*R*r3*x02^2 - 2*R*x01^2*y02 + 2*R*x01*x02*y01 - 2*R*x01*x02*y02 + 2*R*x02^2*y01 - r3^2*y01^2 - 2*r3^2*y01*y02 - r3^2*y02^2 + 2*r3*x01^2*y02 - 2*r3*x01*x02*y01 + 2*r3*x01*x02*y02 - 2*r3*x02^2*y01 + x01^2*y02^2 - 2*x01*x02*y01*y02 + x02^2*y01^2, # eq1
-r2^2*x01^2 - 2*r2^2*x01*x02 - r2^2*x02^2 - r2^2*y01^2 - 2*r2^2*y01*y02 - r2^2*y02^2 + x01^2*y02^2 - 2*x01^2*y02*y2 + x01^2*y2^2 - 2*x01*x02*y01*y02 + 2*x01*x02*y01*y2 - 2*x01*x02*y02*y2 + 2*x01*x02*y2^2 + 2*x01*x2*y01*y02 - 2*x01*x2*y01*y2 + 2*x01*x2*y02^2 - 2*x01*x2*y02*y2 + x02^2*y01^2 + 2*x02^2*y01*y2 + x02^2*y2^2 - 2*x02*x2*y01^2 - 2*x02*x2*y01*y02 - 2*x02*x2*y01*y2 - 2*x02*x2*y02*y2 + x2^2*y01^2 + 2*x2^2*y01*y02 + x2^2*y02^2, # eq2
-r2^2*x01^2 - r2^2*y01^2 + x01^2*y2^2 - 2*x01*x2*y01*y2 + x2^2*y01^2, # eq3
R^2*x01^2 - 2*R*r1*x01^2 - r1^2*y01^2, # eq4
-r2^2*x01^2 + 2*r2^2*x01*x02 - r2^2*x02^2 - r2^2*y01^2 + 2*r2^2*y01*y02 - r2^2*y02^2 + x01^2*y02^2 - 2*x01^2*y02*y2 + x01^2*y2^2 - 2*x01*x02*y01*y02 + 2*x01*x02*y01*y2 + 2*x01*x02*y02*y2 - 2*x01*x02*y2^2 + 2*x01*x2*y01*y02 - 2*x01*x2*y01*y2 - 2*x01*x2*y02^2 + 2*x01*x2*y02*y2 + x02^2*y01^2 - 2*x02^2*y01*y2 + x02^2*y2^2 - 2*x02*x2*y01^2 + 2*x02*x2*y01*y02 + 2*x02*x2*y01*y2 - 2*x02*x2*y02*y2 + x2^2*y01^2 - 2*x2^2*y01*y02 + x2^2*y02^2, # eq5
-4*R^2 + (x01 - x02)^2 + (x01 + x02)^2 + (-y01 + y02)^2 + (y01 + y02)^2, # eq6
-2*R - 2*r2 + sqrt((x01 - x02)^2 + (-y01 + y02)^2) + sqrt((x01 + x02)^2 + (y01 + y02)^2), # eq7
]
end;
r3 = 1.3
iniv = BigFloat[5, 2.38148, 1.38386, 2.19015, 2.52282, 4.54737, 2.22096]
res = nls(H, ini=iniv)
([5.245405918341268, 2.494544851553091, 1.3500234539411795, 2.5099962534726905, 2.655439704703816, 4.756656192448811, 2.5869506037665375], true)
例えば,小円の直径が 2.6 のとき,外円の直径は 10.4908 である。
小円の直径と外円の直径は直線関係ではない(定数倍ではない)。
全てのパラメータは以下のとおりである。
r3 = 1.3; R = 5.24541; r1 = 2.49454; r2 = 1.35002; x2 = 2.51; y2 = 2.65544; x01 = 4.75666; y01 = 2.211; x02 = 2.58695; y02 = 4.56311
術は判読できない部分があるようであるが,山村は最終的に 「外円径 = 2.905×小円径」としている。
しかし,例に挙げた図では,小円の直径が 2.6 のとき,外円の直径は 2.905*2.6 = 7.553 になってしまい,上の数値解と合わない。
function draw(more=false)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
(R, r1, r2, x2, y2, x01, x02) = res[1]
y01 = sqrt(R^2 - x01^2)
y02 = sqrt(R^2 - x02^2)
@printf("小円の直径が %g のとき,外円の直径は %g である。\n", 2r3, 2R)
@printf("r3 = %g; R = %g; r1 = %g; r2 = %g; x2 = %g; y2 = %g; x01 = %g; y01 = %g; x02 = %g; y02 = %g\n",
r3, R, r1, r2, x2, y2, x01, y01, x02, y02)
plot([x01, -x02, -x01, x01], [-y01, y02, y01, -y01], color=:green, lw=0.5)
plot!([-x01, x02, x01, -x01], [-y01, y02, y01, -y01], color=:palevioletred, lw=0.5)
circle(0, 0, R, :firebrick)
circle(0, r1 - R, r1, :magenta)
circle2(x2, y2, r2)
circle(0, R - r3, r3, :blue)
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
hline!([0], color=:gray80, lw=0.5)
vline!([0], color=:gray80, lw=0.5)
point(0, r1 - R, "大円:r1,(0,r1-R)", :magenta, :center, delta=-delta/2)
point(x2, y2, "中円:r2,(x2,y2)", :red, :center, delta=-delta/2)
point(0, R - r3, "小円:r3\n(0,R-r3)", :blue, :center, :bottom, delta=delta/2)
point(x02, y02, "(x02,y02)", :palevioletred, :left, :bottom, delta=delta/2)
point(x01, y01, " (x01,y01)", :palevioletred, :left, :vcenter)
point(-x01, -y01, "(-x01,-y01) ", :palevioletred, :right, :vcenter)
point(-x02, y02, "(-x02,y02)", :green, :right, :bottom, delta=delta/2)
point(x01, -y01, " (x01,-y01)", :green, :left, :vcenter)
point(-x01, y01, "(-x01,y01) ", :green, :right, :vcenter)
point(0, R, "R", :firebrick, :center, :bottom, delta=delta)
plot!(xlims=(-R - 15delta, R + 15delta))
end
end;
draw(true)