算額(その1470)
田村市大越町牧野 見渡神社 安政3年(1856)
街角の数学 Street Wasan ~落書き帳「○△□」~ 299.牧野見渡神社(その3)
http://streetwasan.web.fc2.com/math17.8.17.html
長立円(回転楕円体)の中に,互いに外接し長立円に内接する 2 個の大球と,互いに外接し大球に外接,長立円に内接する 8 個の小球を容れる。長立円の短径が 1 寸のとき,長径はいかほどか。

左は横から見た図,右は上から見た図
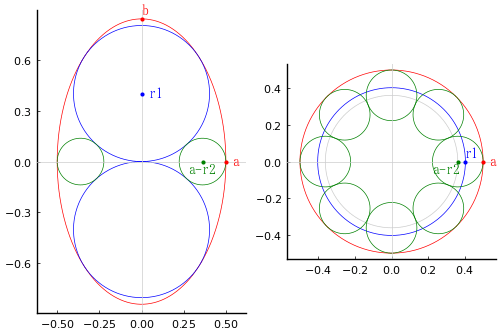
長立円の長径,短径,中心座標を b, a, (0, 0, 0)
大球の半径,中心座標を r1, (0, 0, r1), (0, 0, -r1)
小球の半径,中心座標を r2, (a - r2, 0, 0), ((a - r2)/√2, a - r2)/√2, 0)
とおき,以下の連立方程式を解く。
include("julia-source.txt");
using SymPy
@syms a::poitive, b::poitive,
r1::poitive, r2::poitive
eq1 = (b^2 - a^2)*(a^2 - r1^2)/a^2 - r1^2 # 「算法助術」公式84
eq2 = (a - r2)^2 + r1^2 - (r1 + r2)^2
eq3 = r2 - (a - r2)*sind(Sym(45/2))
res = solve([eq1, eq2, eq3], (r1, r2, b))[2]
res |> println
(-a/2 + a/sqrt(2 - sqrt(2)), a*sqrt(2 - sqrt(2))/(sqrt(2 - sqrt(2)) + 2), 2*a*(2 - sqrt(2))^(3/4)/sqrt(-4*sqrt(2) - 3*sqrt(2)*sqrt(2 - sqrt(2)) + 2*sqrt(2 - sqrt(2)) + 8))
長立円の短径が 1 寸のとき,長径は 1.69162320932629 である。
res[3] |> println
res[3](a => 1).evalf() |> println
2*a*(2 - sqrt(2))^(3/4)/sqrt(-4*sqrt(2) - 3*sqrt(2)*sqrt(2 - sqrt(2)) + 2*sqrt(2 - sqrt(2)) + 8)
1.69162320932629
function draw(a, more=false)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
(r1, r2, b) = (-a/2 + a/sqrt(2 - sqrt(2)), a*sqrt(2 - sqrt(2))/(sqrt(2 - sqrt(2)) + 2), 2*a*(2 - sqrt(2))^(3/4)/sqrt(-4*sqrt(2) - 3*sqrt(2)*sqrt(2 - sqrt(2)) + 2*sqrt(2 - sqrt(2)) + 8))
@printf("長径 = %g; 短径 = %g; a = %g; b = %g; r1 = %g; r2 = %g\n", 2b, 2a, a, b, r1, r2)
p1 = plot()
ellipse(0, 0, a, b, color=:red)
circle22(0, r1, r1, :blue)
circle2(a - r2, 0, r2, :green)
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
hline!([0], color=:gray80, lw=0.5)
vline!([0], color=:gray80, lw=0.5)
point(a - r2, 0, "a-r2", :green, :center, delta=-delta/2)
point(a, 0, " a", :red, :left, :vcenter)
point(0, r1, " r1", :blue, :left, :vcenter)
point(0, b, "b", :red, :left, :bottom, delta=delta/2)
end
p2 = plot()
circle(0, 0, a - r2, :gray80)
circle(0, 0, a)
circle(0, 0, r1, :blue)
rotate(0, a - r2, r2, :green, angle=45)
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
hline!([0], color=:gray80, lw=0.5)
vline!([0], color=:gray80, lw=0.5)
point(a - r2, 0, "a-r2", :green, :right, delta=-delta/2, deltax=delta)
point(a, 0, " a", :red, :left, :vcenter)
point(r1, 0, "r1", :blue, :left, :bottom, delta=delta/2, deltax=-delta/4)
end
plot(p1, p2)
end;
draw(1/2, true)



























