算額(その851)改訂版
算額(その851)は依拠した山村の図が不適切だったことがわかったので,改訂版を書く
九 岩手県水沢市佐倉河 胆沢城八幡神社 弘化2年(1845)
山村善夫:現存 岩手の算額,昭和52年1月30日,熊谷印刷,盛岡市.
http://www.wasan.jp/yamamura/yamamura.html
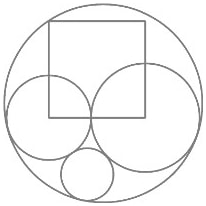
今有如図 03025
https://w.atwiki.jp/sangaku/pages/143.html
キーワード:円4個,外円,ひし形,面積
#Julia, #SymPy, #算額, #和算
大円内に互いに内接・外接する小円 3 個と,菱形を入れる。小円の直径が与えられたとき,黒積を求めよ。
図では,小円,菱形はどれにも接していないが,そんな訳はないだろう。
山村の図では,どれが黒積か明確ではない。「今有如図」でどれが黒積か分かったので,改訂版を書く。

外円の半径と中心座標を R, (0, 0)
小円の半径と中心座標を r, (0, R - r), (x, y)
∠AOB を θ
とおき,以下の連立方程式を解く。
一度に解けないので,まず eq1, eq3 から x,y を求め,結果を eq2 に代入して b を求める。
include("julia-source.txt");
# julia-source.txt ソース https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf
using SymPy
@syms r, R, x, y, a, b
R = b + r
a = sqrt(R^2 - (b - R)^2)
eq1 = x^2 + y^2 - (R - r)^2
eq2 = dist2(0, 2b - R, a, b - R, x, y, r)
eq3 = x^2 + (R - r - y)^2 - 4r^2;
#res = solve([eq1, eq2, eq3], (x, y, b))
res = solve([eq1, eq3], (x, y))[2]
(2*r*sqrt(-(-b + r)*(b + r))/b, -(-b^2 + 2*r^2)/b)
eq12 = eq2(x => res[1], y => res[2]) |> simplify |> numerator |> x -> x/r^2 |> factor
eq12 |> println
(-b + 2*r)*(-3*b^2 - 2*b*r + 4*r^2 - 4*sqrt(b^2 - r^2)*sqrt(b^2 + 2*b*r))
eq12 は(2r - b) という因数を持つので,b = 2r はその解である。また,適解であることが確かめられる。
よって,x, y は,r = 1/2, b = 2r = 1 を代入することにより,√3/2, 1/2 である。
# x
res[1](r => 1//2, b => 1) |> println
sqrt(3)/2
# y
res[2](r => 1//2, b => 1) |> println
1/2
結果としてこの場合には,小円の中心は一辺の長さが 2r の正六角形の頂点である。
黒積は「扇形AOBの面積 - 扇型ACDの面積 - ⊿OCDの面積」の 4 倍である。
∠ACD = 120°,∠AOB = 30° なので,面積 S は 4*(π*R^2*(30/360) - (R - r)*cosd(30)*r/2 - π*r^2*(120/360)) である。
簡約化すると -sqrt(3)*b*r - 4*pi*r^2/3 + pi*(b + r)^2/3 である。
S = 4*(PI*R^2*(30//360) - (R - r)*cosd(Sym(30))*r//2 - PI*r^2*(120//360)) |> simplify
S |> println
-sqrt(3)*b*r - 4*pi*r^2/3 + pi*(b + r)^2/3
術は,小円の直径が 1 のときで,そのとき b も 1 になるので,黒積の数値は 5*pi/12 - √3/2 = 0.4429715352113086
S(b =>1, r => 1//2) |> simplify |> println
-sqrt(3)/2 + 5*pi/12
-sqrt(3)/2 + 5*pi/12
0.4429715352113086
術は円積率=0.76 を使っているので,黒積は「(0.76*10 - sqrt(27))/6」で,計算結果は 0.40064126288222796 となる。
円周率を使うと (pi/4*10 - sqrt(27))/6 = 0.44297153521130844 である。
(pi/4*10 - sqrt(27))/6 は簡約化すると -sqrt(3)/2 + 5*pi/12 となり,上述の式と同じである。
function draw(more=false)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
r = 1/2
b = 2r
x = 2r*sqrt((b - r)*(b + r))/b
y = (b^2 - 2r^2)/b
R = b + r
a = sqrt(R^2 - (b - R)^2)
θ = asind(r/(R - r))
S = -sqrt(3)*b*r - 4*pi*r^2/3 + pi*(b + r)^2/3
@printf("小円の直径が %g のとき,黒積は %g である。\n", 2r, 4S)
@printf("r = %g; x = %g; y = %g; b = %g; a = %g; R = %g; θ = %g\n", r, x, y, b, a, R, θ)
plot([0, a, 0, -a, 0], [-R, b - R, 2b - R, b - R, -R], color=:green, lw=0.5)
circle(0, 0, R)
circle(0, R - r, r, :blue)
circle2(x, y, r, :blue)
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
hline!([0], color=:gray80, lw=0.5)
vline!([0], color=:gray80, lw=0.5)
point(R, 0, " R", :red, :left, :vcenter)
point(x, y, "小円:r,(x,y)", :blue, :center, delta=-delta/2)
θ2 = 30:0.1:90
ax = R.*cosd.(θ2)
ay = R.*sind.(θ2)
θ3 = 90:-0.1:-30
append!(ax, r.*cosd.(θ3))
append!(ay, (R - r) .+ r.*sind.(θ3))
θ4 = 150:-0.1:30
append!(ax, x .+ r.*cosd.(θ4))
append!(ay, y .+ r.*sind.(θ4))
plot!(ax, ay, seriestype=:shape, color=:gray80, fillcolor=:gray80, lw=0.5)
plot!(-ax, ay, seriestype=:shape, color=:gray80, fillcolor=:gray80, lw=0.5)
segment(0, 0, R*cosd(60), R*sind(60), :gray60)
point(0, R, "A", :red, :center, :bottom, delta=delta/2)
point(R*cosd(60), R*sind(60), "B", :red, :left, :bottom, delta=delta/2)
point(0, R - r, "C ", :blue, :right, :vcenter)
point(x/2, (R - r + y)/2, " D", :blue, :left)
segment(0, R - r, x/2, (R - r + y)/2, :gray60)
segment(0,0, 0, R - r, :gray60)
point(0, 0, "O", :red, :center, delta=-delta/2)
point(0, 2b - R, "2b-r ", :green, :right, :vcenter)
point(0, b - R, "b-r ", :green, :right, :vcenter)
point(a, b - R, "(a,b-r) ", :green, :right, :vcenter)
end
end;
draw(true)