算額（その1248）

算額（その1248）

四十九 群馬県安中市板鼻 鷹巣神社 文政11年(1828)
群馬県和算研究会:群馬の算額，上武印刷株式会社，高崎市，1987年3月31日.
キーワード：円2個，楕円2個

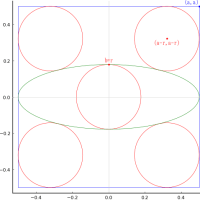
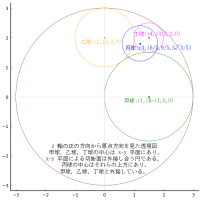
等楕円と等円が 2 個，互いに接し合っている。楕円の長径，短径が与えられたとき，等円の直径を求める術を述べよ。

楕円の長半径，短半径，中心座標を a, b, (0, b)
等円の半径と中心座標を r, (r, 0)
共通接点の座標を (x0, y0)
とおき，以下の連立方程式を解く。

include("julia-source.txt");

using SymPy

@syms a::positive, b::positive, r::positive,
     x0::positive, y0::positive
eq1 = x0^2/a^2 + (y0 - b)^2/b^2 - 1
eq2 = (x0 - r)^2 + y0^2 - r^2
eq3 = -b^2*x0/(a^2*(y0 - b)) + (x0 - r)/y0
res = solve([eq1, eq2, eq3], (r, x0, y0))[2];

等円の半径は，以下の式のようになる。計算の順序を考えると見た目ほどは複雑ではないといえるかもしれない。

res[1]

なお，当然とも言えるが，a, b は勝手にどのような値でも取れるわけではない。
また，算額では想定していない，円と楕円の接点が別の場所になる解もある。

function draw(a, b, more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (r, x0, y0) = (sqrt(2)*sqrt((a^2 + 3*b^2 - sqrt(a^4 - 10*a^2*b^2 + 9*b^4))/(a^2 - b^2))*(3*a^2 - 3*b^2 + sqrt(a^4 - 10*a^2*b^2 + 9*b^4))/(8*a), sqrt(2)*a*sqrt((a^2 + 3*b^2 - sqrt(a^4 - 10*a^2*b^2 + 9*b^4))/(a^2 - b^2))/2, b*(3*a^2 - 3*b^2 + sqrt(a^4 - 10*a^2*b^2 + 9*b^4))/(2*(a^2 - b^2)))
   @printf("a = %g;  b = %g;  r = %g;  x0 = %g;  y0 = %g\n", a, b, r, x0, y0)
   plot()
   #ellipse(0, b, a, b, color=:red)
   #ellipse(0, -b, a, b, color=:red)
   circle2(r, 0, r, :blue)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(r, 0, " 等円:r,(r,0)", :blue, :left, :vcenter)
       point(0, b, "   等楕円:a,b,(0,b)", :red, :left, :vcenter)
       point(x0, y0, "(x0,y0)", :red, :left, :bottom, delta=delta/2)
   end
   ellipse(0, b, a, b, color=:red)
   ellipse(0, -b, a, b, color=:red)
end;

draw(1, 0.25, true)