算額（その1374）

算額（その1374）

神壁算法 天明5年乙巳 秋九月 第二術 關流四傅藤田権平定資六弟子 東都青山 西村治郎右衛門政央
藤田貞資(1789)：神壁算法巻上
http://www.wasan.jp/jinpeki/jinpekisanpo1.pdf
キーワード：球5個，外球，3次元，ソディ・ゴセットの n+1 球定理
#Julia, #SymPy, #算額, #和算

大球の中に，甲球，乙球，丙球，丁球の 4 球を容れる。甲球，乙球，丙球，丁球の直径が 3 寸，2 寸，1.2寸， 1 寸のとき，大球の直径はいかほどか。

注：甲球，乙球，丙球，丁球は互いに外接し，それぞれは大球に内接している。

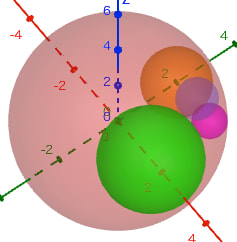
この問題を解くには，2 次元平面上で 4 個の円の半径 rᵢ から計算される曲率 kᵢ = 1/rᵢ の関係についてのデカルトの円定理を3次元に拡張したものを使う。

一般的には，「ソディ・ゴセットの n+1 球定理」https://ikuro-kotaro.sakura.ne.jp/koramu/8023_p2.htm というもので，n 次元空間では，互いに接する n + 2 個の球の間に

　　　n*(k₁² + k₂² + k₃² + ... + kₙ₊₂²) = (k₁ + k₂ + k₃ + ... ± kₙ₊₂)²

が成り立つ。

n = 2 の場合がデカルトの円定理である。

本問は n = 3 の場合であり，以下の式が成り立つ。
互いに外接する 4 個の球のとき，k₅² の符号がマイナスの場合は 4 個の球は 5 番目の球に内接し，プラスの場合は 5 番目の球に外接する。

　　　3(k₁² + k₂² + k₃² + k₄² + kₙ₊₂²) = (k₁ + k₂ + k₃ + k₄ ± k₅)²

include("julia-source.txt");
# julia-source.txt ソース　https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf

4 個の球が 5 番目の球に内接する場合 --- 　5 番目の球の半径

@syms r1, r2, r3, r4, r5, k1, k2, k3, k4, k5
eq01 = 3(k1^2 + k2^2 + k3^2 + k4^2 + k5^2) - (k1 + k2 + k3 + k4 - k5)^2;
K5 = solve(eq01, k5)[2]  # 2 of 2
K5 |> println

   -k1/2 - k2/2 - k3/2 - k4/2 + sqrt(3)*sqrt(-k1^2 + 2*k1*k2 + 2*k1*k3 + 2*k1*k4 - k2^2 + 2*k2*k3 + 2*k2*k4 - k3^2 + 2*k3*k4 - k4^2)/2

1/K5(k1 => 1/r1, k2 => 1/r2, k3 => 1/r3, k4 => 1/r4)(r1 => 3//2, r2 => 1, r3 => 12//20, r4 => 1//2) |> println

   3

4 個の球が 5 番目の球に外接する場合 --- 5 番目の球の半径

eq02 = 3(k1^2 + k2^2 + k3^2 + k4^2 + k5^2) - (k1 + k2 + k3 + k4 + k5)^2;
K6 = solve(eq02, k5)[2]
K6 |> println

   k1/2 + k2/2 + k3/2 + k4/2 + sqrt(3)*sqrt(-k1^2 + 2*k1*k2 + 2*k1*k3 + 2*k1*k4 - k2^2 + 2*k2*k3 + 2*k2*k4 - k3^2 + 2*k3*k4 - k4^2)/2

1/K6(k1 => 1/r1, k2 => 1/r2, k3 => 1/r3, k4 => 1/r4)(r1 => 3//2, r2 => 1, r3 => 12//20, r4 => 1//2) |> println

   3/17

以下の関数は，4個の球の半径 r1, r2, r3, r4 を与えると，4 球が内接する球と4 球が外接する球の両方の半径を返す。

function radius_of_fifth_sphere(r1, r2, r3, r4)
   (k1, k2, k3, k4) = 1 ./ (r1, r2, r3, r4)
   #return 1/(-k1/2 - k2/2 - k3/2 - k4/2 + sqrt(3)*sqrt(-k1^2 + 2*k1*(k2 + k3 + k4) - k2^2 + 2*k2*(k3 + k4) - k3^2 + 2*k3*k4 - k4^2)/2),
   #       1/( k1/2 + k2/2 + k3/2 + k4/2 + sqrt(3)*sqrt(-k1^2 + 2*k1*(k2 + k3 + k4) - k2^2 + 2*k2*(k3 + k4) - k3^2 + 2*k3*k4 - k4^2)/2)
   (a, b) = (k1/2 + k2/2 + k3/2 + k4/2, sqrt(3)*sqrt(-k1^2 + 2*k1*(k2 + k3 + k4) - k2^2 + 2*k2*(k3 + k4) - k3^2 + 2*k3*k4 - k4^2)/2)
   return 1/(b - a), 1/(b + a)
end;

問では，甲球，乙球，丙球，丁球の直径が 3 寸，2 寸，1.2寸，1 寸のときなので，4 球が内接する大球の半径は 3 寸と計算される。

radius_of_fifth_sphere(3/2, 2/2, 1.2/2, 1/2)

   (3.0000000000000027, 0.17647058823529413)

算額の問は，大球の直径だけを問うているので，「大球の直径は 6 寸」で完了である。

以下では，図を描くために必要なパラメータを求める。

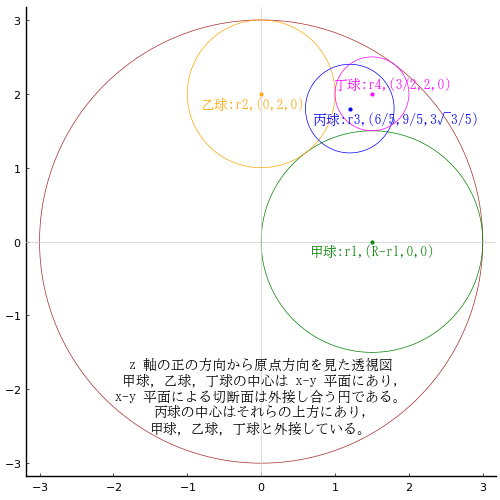
座標軸は任意に設定できるので，大球の中心を原点とし，甲球の中心は x 軸上にあり，乙球は x−y 平面上にあるように設定する。後に明らかになるが，乙球の中心は y 軸上にある。
大球の半径と中心座標を R, (0, 0, 0)
甲球の半径と中心座標を r1, (R - r1, 0, 0)
乙球の半径と中心座標を r2, (x2, y2, 0)
丙球の半径と中心座標を r3, (x3, y3, z3)
丁球の半径と中心座標を r4, (x4, y4, z4)
とおき，以下の連立方程式を（逐次的に）解く。

using SymPy
@syms R::positive, r1::positive,
     r2::positive, x2::positive, y2::positive,
     r3::positive, x3::positive, y3::positive, z3::positive,
     r4::positive, x4::positive, y4::positive, z4::positive;

eq1 = x2^2 + y2^2 - (R - r2)^2
eq2 = x3^2 + y3^2 + z3^2 - (R - r3)^2
eq3 = x4^2 + y4^2 + z4^2 - (R - r4)^2
eq4 = (R - r1)^2 + y2^2 - (r1 + r2)^2
eq5 = (R - r1 - x3)^2 + y3^2 + z3^2 - (r1 + r3)^2
eq6 = (R - r1 - x4)^2 + y4^2 + z4^2 - (r1 + r4)^2
eq7 = (x2 - x3)^2 + (y2 - y3)^2 + z3^2 - (r2 + r3)^2
eq8 = (x2 - x4)^2 + (y2 - y4)^2 + z4^2 - (r2 + r4)^2
eq9 = (x3 - x4)^2 + (y3 - y4)^2 + (z3 - z4)^2 - (r3 + r4)^2;
# res = solve([eq1, eq2, eq3, eq4, eq5, eq6, eq7, eq8, eq9], (R, x2, y2, x3, y3, z3, x4, y4, z4))

1.　R を求める

「ソディ・ゴセットの n+1 球定理」から，R = 3 なので，甲球の半径と中心座標は 1.5, (1.5, 0, 0) である。

2.　x2, y2 を求める

eq1, eq4 を解いて，x2, y2 を求める。
乙球の半径と中心座標は 1, (0, 2, 0) である。

res = solve([eq1, eq4], (x2, y2))[1]

   (sqrt(2)*sqrt(R^2 - R*r1 - R*r2 - r1*r2), sqrt(R + r2)*sqrt(-R + 2*r1 + r2))

x2
res[1](R => 3, r1 => 3//2, r2 => 2//2) |> println
y2
res[2](R => 3, r1 => 3//2, r2 => 2//2) |> println

   0
   2

3.　x3, y3, z3 を求める

eq2, eq5, eq7 を解いて，x3, y3, z3 を求める。
丙球の半径と中心座標は 0.6, (6/5, 9/5, 3√3/5) である。

res2 = solve([eq2, eq5, eq7], (x3, y3, z3))[1]  # 1 of 2

   ((-R^2 + R*r1 + R*r3 + r1*r3)/(-R + r1), (-R^3 + R^2*r1 + 2*R^2*r3 + 2*R^2*x2 - 2*R*r1*r3 - 2*R*r1*x2 + R*r2^2 + 2*R*r2*r3 - 2*R*r3*x2 - R*x2^2 - R*y2^2 - r1*r2^2 - 2*r1*r2*r3 - 2*r1*r3*x2 + r1*x2^2 + r1*y2^2)/(2*y2*(-R + r1)), -sqrt(-R^6/4 + R^5*r1/2 + R^5*r3 + R^5*x2 - R^4*r1^2/4 - 2*R^4*r1*r3 - 2*R^4*r1*x2 + R^4*r2^2/2 + R^4*r2*r3 - R^4*r3^2 - 3*R^4*r3*x2 - 3*R^4*x2^2/2 - R^4*y2^2/2 + R^3*r1^2*r3 + R^3*r1^2*x2 - R^3*r1*r2^2 - 2*R^3*r1*r2*r3 + 2*R^3*r1*r3^2 + 4*R^3*r1*r3*x2 + 3*R^3*r1*x2^2 + R^3*r1*y2^2 - R^3*r2^2*r3 - R^3*r2^2*x2 - 2*R^3*r2*r3^2 - 2*R^3*r2*r3*x2 + 2*R^3*r3^2*x2 + 3*R^3*r3*x2^2 + R^3*r3*y2^2 + R^3*x2^3 + R^3*x2*y2^2 + R^2*r1^2*r2^2/2 + R^2*r1^2*r2*r3 - R^2*r1^2*r3^2 - R^2*r1^2*r3*x2 - 3*R^2*r1^2*x2^2/2 - R^2*r1^2*y2^2/2 + 2*R^2*r1*r2^2*r3 + 2*R^2*r1*r2^2*x2 + 4*R^2*r1*r2*r3^2 + 4*R^2*r1*r2*r3*x2 - 2*R^2*r1*r3*x2^2 + 2*R^2*r1*r3*y2^2 - 2*R^2*r1*x2^3 - 2*R^2*r1*x2*y2^2 - R^2*r2^4/4 - R^2*r2^3*r3 - R^2*r2^2*r3^2 + R^2*r2^2*r3*x2 + R^2*r2^2*x2^2/2 + R^2*r2^2*y2^2/2 + 2*R^2*r2*r3^2*x2 + R^2*r2*r3*x2^2 + R^2*r2*r3*y2^2 - R^2*r3^2*x2^2 - R^2*r3*x2^3 - R^2*r3*x2*y2^2 - R^2*x2^4/4 - R^2*x2^2*y2^2/2 - R^2*y2^4/4 - R*r1^2*r2^2*r3 - R*r1^2*r2^2*x2 - 2*R*r1^2*r2*r3^2 - 2*R*r1^2*r2*r3*x2 - 2*R*r1^2*r3^2*x2 - R*r1^2*r3*x2^2 - 3*R*r1^2*r3*y2^2 + R*r1^2*x2^3 + R*r1^2*x2*y2^2 + R*r1*r2^4/2 + 2*R*r1*r2^3*r3 + 2*R*r1*r2^2*r3^2 - R*r1*r2^2*x2^2 - R*r1*r2^2*y2^2 - 2*R*r1*r2*r3*x2^2 - 2*R*r1*r2*r3*y2^2 - 2*R*r1*r3^2*x2^2 - 4*R*r1*r3^2*y2^2 + R*r1*x2^4/2 + R*r1*x2^2*y2^2 + R*r1*y2^4/2 - r1^2*r2^4/4 - r1^2*r2^3*r3 - r1^2*r2^2*r3^2 - r1^2*r2^2*r3*x2 + r1^2*r2^2*x2^2/2 + r1^2*r2^2*y2^2/2 - 2*r1^2*r2*r3^2*x2 + r1^2*r2*r3*x2^2 + r1^2*r2*r3*y2^2 - r1^2*r3^2*x2^2 + r1^2*r3*x2^3 + r1^2*r3*x2*y2^2 - r1^2*x2^4/4 - r1^2*x2^2*y2^2/2 - r1^2*y2^4/4)/(y2*(-R + r1)))

x3
res2[1](R => 3, r1 => 3//2, r2 => 2//2, r3 => 12//20) |> println
y3
res2[2](R => 3, r1 => 3//2, r2 => 2//2, r3 => 12//20, x2 => 0, y2 => 2) |> println
z3
res2[3](R => 3, r1 => 3//2, r2 => 2//2, r3 => 12//20, x2 => 0, y2 => 2) |> println

   6/5
   9/5
   3*sqrt(3)/5

4.　x4,y4,z4 を求める

eq3, eq6, eq8 を解いて，x4, y4, z4 を求める。
丁球の半径と中心座標は 0.5, (3/2, 2, 0) である。

res3 = solve([eq3, eq6, eq8], (x4, y4, z4))[1]  # 1 of 2

   ((-R^2 + R*r1 + R*r4 + r1*r4)/(-R + r1), (-R^3 + R^2*r1 + 2*R^2*r4 + 2*R^2*x2 - 2*R*r1*r4 - 2*R*r1*x2 + R*r2^2 + 2*R*r2*r4 - 2*R*r4*x2 - R*x2^2 - R*y2^2 - r1*r2^2 - 2*r1*r2*r4 - 2*r1*r4*x2 + r1*x2^2 + r1*y2^2)/(2*y2*(-R + r1)), -sqrt(-R^6/4 + R^5*r1/2 + R^5*r4 + R^5*x2 - R^4*r1^2/4 - 2*R^4*r1*r4 - 2*R^4*r1*x2 + R^4*r2^2/2 + R^4*r2*r4 - R^4*r4^2 - 3*R^4*r4*x2 - 3*R^4*x2^2/2 - R^4*y2^2/2 + R^3*r1^2*r4 + R^3*r1^2*x2 - R^3*r1*r2^2 - 2*R^3*r1*r2*r4 + 2*R^3*r1*r4^2 + 4*R^3*r1*r4*x2 + 3*R^3*r1*x2^2 + R^3*r1*y2^2 - R^3*r2^2*r4 - R^3*r2^2*x2 - 2*R^3*r2*r4^2 - 2*R^3*r2*r4*x2 + 2*R^3*r4^2*x2 + 3*R^3*r4*x2^2 + R^3*r4*y2^2 + R^3*x2^3 + R^3*x2*y2^2 + R^2*r1^2*r2^2/2 + R^2*r1^2*r2*r4 - R^2*r1^2*r4^2 - R^2*r1^2*r4*x2 - 3*R^2*r1^2*x2^2/2 - R^2*r1^2*y2^2/2 + 2*R^2*r1*r2^2*r4 + 2*R^2*r1*r2^2*x2 + 4*R^2*r1*r2*r4^2 + 4*R^2*r1*r2*r4*x2 - 2*R^2*r1*r4*x2^2 + 2*R^2*r1*r4*y2^2 - 2*R^2*r1*x2^3 - 2*R^2*r1*x2*y2^2 - R^2*r2^4/4 - R^2*r2^3*r4 - R^2*r2^2*r4^2 + R^2*r2^2*r4*x2 + R^2*r2^2*x2^2/2 + R^2*r2^2*y2^2/2 + 2*R^2*r2*r4^2*x2 + R^2*r2*r4*x2^2 + R^2*r2*r4*y2^2 - R^2*r4^2*x2^2 - R^2*r4*x2^3 - R^2*r4*x2*y2^2 - R^2*x2^4/4 - R^2*x2^2*y2^2/2 - R^2*y2^4/4 - R*r1^2*r2^2*r4 - R*r1^2*r2^2*x2 - 2*R*r1^2*r2*r4^2 - 2*R*r1^2*r2*r4*x2 - 2*R*r1^2*r4^2*x2 - R*r1^2*r4*x2^2 - 3*R*r1^2*r4*y2^2 + R*r1^2*x2^3 + R*r1^2*x2*y2^2 + R*r1*r2^4/2 + 2*R*r1*r2^3*r4 + 2*R*r1*r2^2*r4^2 - R*r1*r2^2*x2^2 - R*r1*r2^2*y2^2 - 2*R*r1*r2*r4*x2^2 - 2*R*r1*r2*r4*y2^2 - 2*R*r1*r4^2*x2^2 - 4*R*r1*r4^2*y2^2 + R*r1*x2^4/2 + R*r1*x2^2*y2^2 + R*r1*y2^4/2 - r1^2*r2^4/4 - r1^2*r2^3*r4 - r1^2*r2^2*r4^2 - r1^2*r2^2*r4*x2 + r1^2*r2^2*x2^2/2 + r1^2*r2^2*y2^2/2 - 2*r1^2*r2*r4^2*x2 + r1^2*r2*r4*x2^2 + r1^2*r2*r4*y2^2 - r1^2*r4^2*x2^2 + r1^2*r4*x2^3 + r1^2*r4*x2*y2^2 - r1^2*x2^4/4 - r1^2*x2^2*y2^2/2 - r1^2*y2^4/4)/(y2*(-R + r1)))

x4
res3[1](R => 3, r1 => 3//2, r2 => 2//2, r3 => 12//20, r4 => 1//2) |> println
y4
res3[2](R => 3, r1 => 3//2, r2 => 2//2, r3 => 12//20, r4 => 1//2, x2 => 0, y2 => 2) |> println
z4
res3[3](R => 3, r1 => 3//2, r2 => 2//2, r3 => 12//20, r4 => 1//2, x2 => 0, y2 => 2) |> println

   3/2
   2
   0

以下は，図を描くためのプログラムである。3次元の図は GeoGebra によって描いた。

function radius_of_fifth_sphere(r1, r2, r3, r4)
   (k1, k2, k3, k4) = 1 ./ (r1, r2, r3, r4)
   (a, b) = (k1/2 + k2/2 + k3/2 + k4/2, sqrt(3)*sqrt(-k1^2 + 2*k1*(k2 + k3 + k4) - k2^2 + 2*k2*(k3 + k4) - k3^2 + 2*k3*k4 - k4^2)/2)
   return 1/(b - a), 1/(b + a)
end;

function draw(more)
    pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (r1, r2, r3, r4) = (3/2, 2/2, 1.2/2, 1/2)
   (R, junk) = radius_of_fifth_sphere(r1, r2, r3, r4)
   (x2, y2) = (0, 2)
   (x3, y3, z3) = (6/5, 9/5, 3√3/5)
   (x4, y4, z4) = (3/2, 2, 0)
   plot()
   circle(0, 0, R, :brown)
   circle(R - r1, 0, r1, :green)
   circle(x2, y2, r2, :orange)
   circle(x3, y3, r3, :blue)
   circle(x4, y4, r4, :magenta)
   if more == true
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
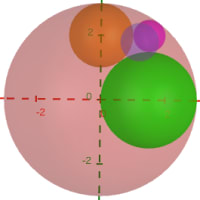
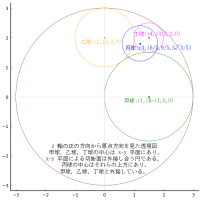
       point(0, -1.57, "z 軸の正の方向から原点方向を見た透視図\n甲球，乙球，丁球の中心は x-y 平面にあり,\nx-y 平面による切断面は外接し合う円である。\n丙球の中心はそれらの上方にあり,\n甲球，乙球，丁球と外接している。", :black, :center, mark=false)
       point(R - r1, 0, "甲球:r1,(R-r1,0,0)", :green, :center, delta=-delta/2)
       point(0, 2, "乙球:r2,(0,2,0)", :orange, :right, delta=-delta/2, deltax=7delta)
       point(6/5, 9/5, "丙球:r3,(6/5,9/5,3√3/5)", :blue, :left, delta=-delta/2, deltax=-6delta)
       point(3/2, 2, "丁球:r4,(3/2,2,0)", :magenta, :left, :bottom, delta=delta/2, deltax=-6delta)
   end
end;

draw(true)