算額（その1516）

算額（その1516）

八十五 岩手県一関市室根町折壁字天王前 彌榮神社 明治16年(1883)
山村善夫：現存 岩手の算額，昭和52年1月30日，熊谷印刷，盛岡市.
http://www.wasan.jp/yamamura/yamamura.html

今有如図 03067
https://w.atwiki.jp/sangaku/pages/286.html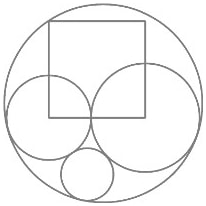

キーワード：円4,外円，正方形
#Julia, #SymPy, #算額, #和算

外円の中に，乾円，兌円，離円，正方形を容れる。乾円の直径は，離円の直径の 195/500 倍，正方形の一辺の長さは離円と乾円の直径の半分である。兌円の直径はいかほどか。

注1：山村の図では正方形は外円と 2 点で接しているが，乾円と離円の中心が残りの頂点になるべきなので（村山の図ではそのように描かれていないが），そのような場合には図は左右対称になり，必然的に乾円と離円は合同になり，兌円の中心は外円の中心線上にあることになり，問題にならない。また，「乾円の直径は，離円の直径の 195/500 倍」なのだから，乾円は離円より小さいことになるが，山村の図では逆になっている。「今有如図」では，どれがどの円なのかが図に描かれていないので参考にはならないが，山村の解釈は間違っている。また，術の解説も妥当なものではない。術自体もおかしいが。
注2：問題文では，基準となる円の絶対的な大きさが書かれていないので，「兌円の直径はいかほどか」は術も「四分1」と書かれており相対的なものであるが，何に対しての相対値化が明示されていない。

外円の半径と中心座標を R, (0, 0)
離円の半径と中心座標を r1, (x1, y1)
乾円の半径と中心座標を r2, (x2, y2); y2 = y1
兌円の半径と中心座標を r3, (x3, y3)
正方形の一辺の長さを a
とおき，以下の連立方程式を解く。

include("julia-source.txt")
# julia-source.txt ソース　https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf

using SymPy
@syms R, a, x0, r1, x1, y1, r2, x2, y2, r3, x3, y3
r2 = r1*195//500
a = r1 + r2
y2 = y1
eq1 = x1^2 + y1^2 - (R - r1)^2
eq2 = x2^2 + y2^2 - (R - r2)^2
eq3 = x3^2 + y3^2 - (R - r3)^2
eq4 = (x1 - x3)^2 + (y1 - y3)^2 - (r1 + r3)^2
eq5 = (x2 - x3)^2 + (y2 - y3)^2 - (r2 + r3)^2
eq6 = x1 - x2 - a
eq7 = (sqrt(R^2 - x2^2) - y2) - (r1 + r2);
# solve([eq1, eq2, eq3, eq4, eq5, eq6, eq7], (R, x1, y1, x2, r3, x3, y3))

function H(u)
    (R, x1, y1, x2, r3, x3, y3) = u
    return [
        x1^2 + y1^2 - (R - r1)^2,  # eq1
        x2^2 + y1^2 - (R - 39*r1/100)^2,  # eq2
        x3^2 + y3^2 - (R - r3)^2,  # eq3
        -(r1 + r3)^2 + (x1 - x3)^2 + (y1 - y3)^2,  # eq4
        -(39*r1/100 + r3)^2 + (x2 - x3)^2 + (y1 - y3)^2,  # eq5
        -139*r1/100 + x1 - x2,  # eq6
        -139*r1/100 - y1 + sqrt(R^2 - x2^2),  # eq7
    ]
end;
r1 = 1/2
iniv = BigFloat[0.74, 0.17, -0.17, -0.52, 0.14, -0.38, -0.47]
res = nls(H, ini=iniv)

    ([0.7414808299927744, 0.17460193791683998, -0.1668147311531064, -0.52039806208316, 0.1354422352837994, -0.38483674087676983, -0.4681703334772241], true)

離円の半径が 1/2 のとき，兌円の半径は 0.1354422352837994となり，離円の大きさの 0.1354422352837994/0.5 = 0.2708844705675988 で，「1/4」には一致しない。

全てのパラメータは以下のとおりである。

R = 0.741481;  r1 = 0.5;  x1 = 0.174602;  y1 = -0.166815;  r2 = 0.195;  x2 = -0.520398;  y2 = -0.166815;  r3 = 0.135442;  x3 = -0.384837;  y3 = -0.46817

function draw(r1, more=false)
    pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
    (R, x1, y1, x2, r3, x3, y3) = [10, 3.70185, -1.73789, -6, 2.43359, -2.88951, -7]
    (R, x1, y1, x2, r3, x3, y3) = res[1]
    y2 = y1
    r2 = r1*195/500
    @printf("R = %g;  r1 = %g;  x1 = %g;  y1 = %g;  r2 = %g;  x2 = %g;  y2 = %g;  r3 = %g;  x3 = %g;  y3 = %g\n", R, r1, x1, y1, r2, x2, y2, r3, x3, y3)
    plot([x2, x1, x1, x2, x2], [y2, y2, sqrt(R^2 - x2^2), sqrt(R^2 - x2^2), y2], color=:orange, lw=0.5)
    circle(0, 0, R, :green)
    circle(x1, y1, r1)
    circle(x2, y2, r2, :blue)
    circle(x3, y3, r3, :magenta)
    if more
        delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
        hline!([0], color=:gray80, lw=0.5)
        vline!([0], color=:gray80, lw=0.5)
        point(x1, y1, "離円", :red, :center, delta=-delta)
        point(x2, y2, "乾円", :blue, :center, delta=-delta)
        point(x3, y3, "兌円", :magenta, :center, delta=-delta)
        point(0, R, "R", :green, :center, :bottom, delta=delta)
    end
end;

draw(1/2, true)