算額(その617)
三重県四日市市 神明神社 寛政2年(1790)
「三重県に現存する算額の研究」福島完(2007/2/13)
https://mie-u.repo.nii.ac.jp/?action=repository_uri&item_id=7216
問題文2
菱形の中に,大円 1 個,小円 2 個が入っている。菱形の面積から3個の円の面積を除いた面積(A),菱形の対角線の長さの和(B)と,大円と小円の直径の差(C)が与えられているとき,小円の直径を求めよ。
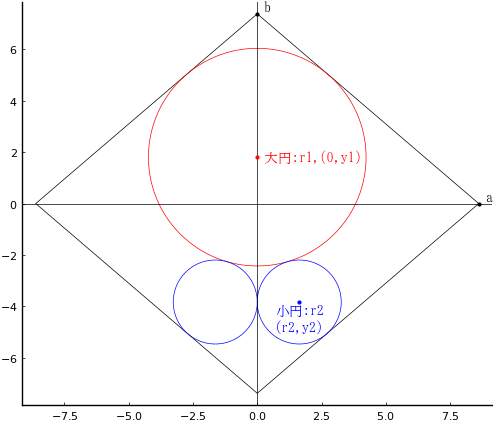
菱形の対角線 2a, 2b (a > b),大円と小円の半径をそれぞれ r1, r2 とする。
以下の方程式を解く。
include("julia-source.txt");
using SymPy
@syms r1::positive, y1::positive, r2::positive, y2::negative, a::positive, b::positive,
A::positive, B::positive, C::positive;
円周率 = 3.16 # 円積率 3.16/4 = 0.79
eq1 = r2^2 + (y1 - y2)^2 - (r1 + r2)^2
eq2 = distance(0, b, a, 0, 0, y1) - r1^2
eq3 = distance(0, -b, a, 0, r2, y2) - r2^2
eq4 = 2a*b - 円周率*r1^2 - 2円周率*r2^2 - A
eq5 = 2a + 2b - B
eq6 = 2r1 - 2r2 - C;
using NLsolve
function nls(func, params...; ini = [0.0])
if typeof(ini) <: Number
r = nlsolve((vout, vin) -> vout[1] = func(vin[1], params..., [ini]), ftol=1e-14)
v = r.zero[1]
else
r = nlsolve((vout, vin)->vout .= func(vin, params...), ini, ftol=1e-14)
v = r.zero
end
return v, r.f_converged
end;
function H(u)
(a, b, r1, y1, r2, y2) = u
return [
r2^2 - (r1 + r2)^2 + (y1 - y2)^2, # eq1
a^2*b^2*(b - y1)^2/(a^2 + b^2)^2 - r1^2 + (-b*(a^2 + b*y1)/(a^2 + b^2) + y1)^2, # eq2
-r2^2 + (-a*(a*r2 + b^2 + b*y2)/(a^2 + b^2) + r2)^2 + (-b*(-a^2 + a*r2 + b*y2)/(a^2 + b^2) + y2)^2, # eq3
2*a*b - 3.16*r1^2 - 6.32*r2^2 - 53.7, # eq4
2*a + 2*b - 32, # eq5
2*r1 - 2*r2 - 5.2, # eq6
]
end;
(A, B, C) = (53.7, 32, 5.2)
iniv = BigFloat[8.62, 7.38, 4.23, 1.81, 1.63, -3.83]
res = nls(H, ini=iniv)
(BigFloat[8.618869516619060933261217496129591164127618589189709440245477710397030837896864, 7.381130483380939066738782503870408835872381410810290559754522289595245106897612, 4.234238957828194708369843972428936199044440731565763308078691436517181518285074, 1.806377116536225577423953366326376812684128330422196332266830152186767547254349, 1.634238957828194619552002002416412965153907284300138308078691438199894855227677, -3.829959998582366768106243609407652459638817222378998651702439496268955544637784], true)
菱形の面積から3個の円の面積を除いた面積(A) = 53.7
菱形の対角線の長さの和(B) = 32
大円と小円の直径の差(C) = 5.2
のとき,
小円の直径 = 3.26848
その他のパラメータは以下の通りである。
a = 8.61887; b = 7.38113; r1 = 4.23424; y1 = 1.80638; r2 = 1.63424; y2 = -3.82996
function draw(more=false)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
(A, B, C) = (53.7, 32, 5.2)
(a, b, r1, y1, r2, y2) = res[1]
@printf("菱形の面積から3個の円の面積を除いた面積(A) = %g\n", A)
@printf("菱形の対角線の長さの和(B) = %g\n", B)
@printf("大円と小円の直径の差(C) = %g\n", C)
@printf("小円の直径 = %g; a = %g; b = %g; r1 = %g; y1 = %g; r2 = %g; y2 = %g\n", 2r2, a, b, r1, y1, r2, y2)
plot([a, 0, -a, 0, a], [0, b, 0, -b, 0], color=:black, lw=0.5)
circle(0, y1, r1)
circle(r2, y2, r2, :blue)
circle(-r2, y2, r2, :blue)
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
vline!([0], color=:black, lw=0.5)
hline!([0], color=:black, lw=0.5)
point(0, y1, " 大円:r1,(0,y1)", :red, :left, :vcenter)
point(r2, y2, "小円:r2\n(r2,y2)", :blue, :center, delta=-delta/2)
point(0, b, " b", :black, :left, :bottom)
point(a, 0, " a", :black, :left, :bottom)
end
end;



























